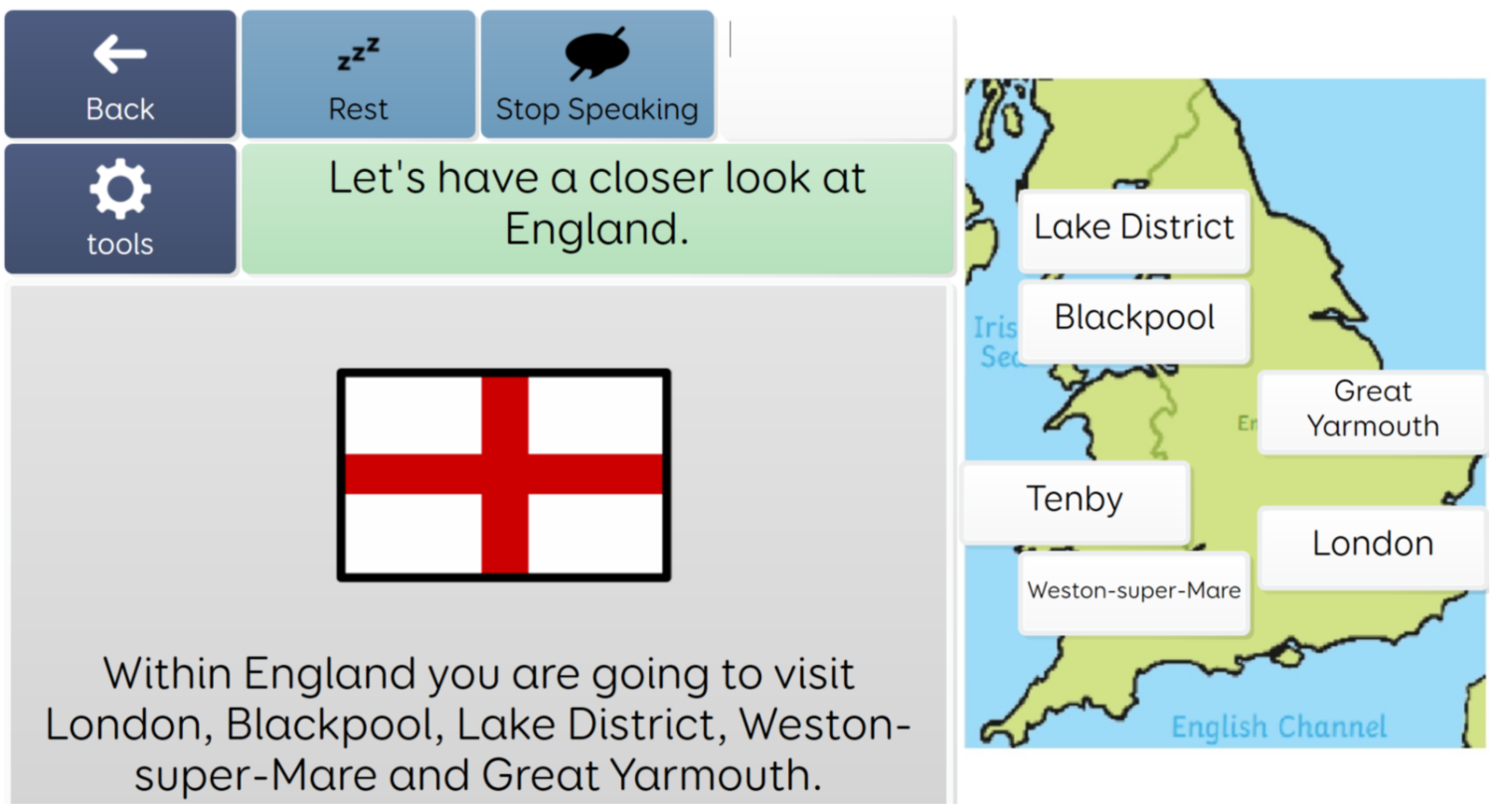
A new look at teaching maths to students who have communication and physical disabilities: Moving beyond counting.
Article by: Marion Stanton (2025), MA, PGCE, Adv. Dip. Ed. Special, AAC Level 7, MCCT
Head of Education for CandLE Limited
There is clear evidence that students with communication and physical disabilities encounter difficulties with developing their arithmetic skills (Rooijen et al, 2015). I have spent many years observing students struggling with early counting to 10 and being rote taught the same concepts every day. I have witnessed the same students being taught the same basic number skills year after year, which every day they appear to forget.
Despite this, in many of these cases the students have not been offered more complex maths because of the belief that they will not be able to grasp maths concepts without basic number skills. I have concluded that we need to look a little deeper into what support students with complex access need to enable them to have a richer and more engaging experience with mathematics.
First some case study examples. All of these students have good cognition and language understanding:
-
- Michelle is in year 9 and attends a mainstream school. She has Cerebral Palsy and is non-speaking. In observing a lesson she attended on function machines, it was clear that she understood the purpose of a function machine and was able to use her communication aid to indicate which direction required an addition or a subtraction and was correct every time. However, when the task was to add 3 to 17 she errored. The non-disabled girl in front of her was able to complete the operation successfully because she had the use of her fingers to enable counting by saying 17 and then putting 3 fingers up and counting on from 17. Michelle does not have the motor skills to use her fingers in this way.
- David is 20 years old and is receiving support for maths and literacy which he has struggled to achieve proficiency in. He has not had access to the National Curriculum because his special schools did not offer it. The functional skills courses that he was offered focus on the areas of English and maths that student who rely on AAC (Augmentative and Alternative Communication) find difficult because of the verbal and motor skill demands of the programs of study. He found it difficult to add 7 + 3 but was able to conceptualize borrowing and carrying from the correct place value position and to identify the correct operation to use.
- Ben is in year 9 in a mainstream school but was in a special school until year 6. It is understood that he only received basic number support prior to entering mainstream. He can demonstrate that algebraic equations require the same action on both sides and that like terms need combining to simplify the expression. However, he finds addition and subtraction under 10 difficult.
- Andy is in year 4 in a mainstream primary school. He can speak but has severe motor restrictions. He shows full understanding of maths concepts, He knows greater and less than. He can indicate where to borrow from or carry to in 3 place value operations. He can place the numerals appropriately in a 3-place value template. However, He struggles with adding numerals, even under 10. He finds doubling (what is double 2) easier than ‘what is 2 +2?’.
- Hal is in year 6 in a mainstream primary school. He was struggling with number despite have a good grasp of maths concepts such as more and less, shapes, which operation is needed for a calculation. We started a project with him whereby we did not ask him to use number bonds or even count independently. We worked on all the other skills in mathematics such as understanding shape, learning mathematical rules and applying them, real world situations that needed a mathematical solution. He blossomed! He might not be able to conserve to 4 but he was very clear that a square has 4 corners and 4 sides and that a rectangle had the same but that 2 sides were longer than the other 2. This alternative route to number began to build his confidence and he made significant progress.
- Fergus is in year 2 in a mainstream primary school. He has cerebral palsy and struggles to grasp, hold and manipulate objects. His TAs are trying to help him to have the manipulatives experience that we recognize as underpinning understanding of number. He cannot manipulate objects independently, so his TAs use guided physical support. It doesn’t work in the same way as it would for a non-disabled child as he is so focused on the physical demands of the task that he forgets the numbers that he needs to be learning.
All these students, and many more I have worked with, are showing that they can grasp complex concepts in mathematics but struggle with basic number. Is continuing to repeat basic number drills, sometimes for many years, that do not result in many of these students gaining number skills the correct way forward? Could there be underlying reasons why number eludes students who have otherwise good cognition. For those students who have learning difficulties affecting their cognition is there another way they can engage with number to make the experience more rewarding and meaningful?
Literature Review
Flores et al (2023) found a direct relationship between mathematical performance and motor skills. They emphasize the importance of posture, grip, vision and motor control in enabling the very young child to develop their cognition. They identify an interrelationship between motor and cognitive development evidenced by neuroimaging of the prefrontal cortex and the cerebellum. Both the gross motor skills of jumping, sliding, running and posture control and the fine motor skills using the small muscle movements of the fingers and hands and the processing of visual and spatial stimuli are identified as important for the development of basic numerical representations.
Critten et al (2018) found that, although it is known that visual spatial ability, associated with non-verbal IQ, is a predictor of performance in mathematics, very little research has been carried out on the roles that difficulties in this area may impact on the development of mathematics skills in children with cerebral palsy. They examined the role of memory, mental rotation (spatial awareness) and non-verbal reasoning and whether cognitive load and the need to switch attention between tasks made the acquisition of maths skills more difficult for students with cerebral palsy.
They found that poor visual-spatial awareness in students with CP did correlate with delayed acquisition of maths skills and that tasks involving active processing resulted in worse performance.
Rooijen et al (2015) Found a strong correlation between working memory deficits and executive function difficulty with delayed acquisition of the ability to develop early numeracy skills.
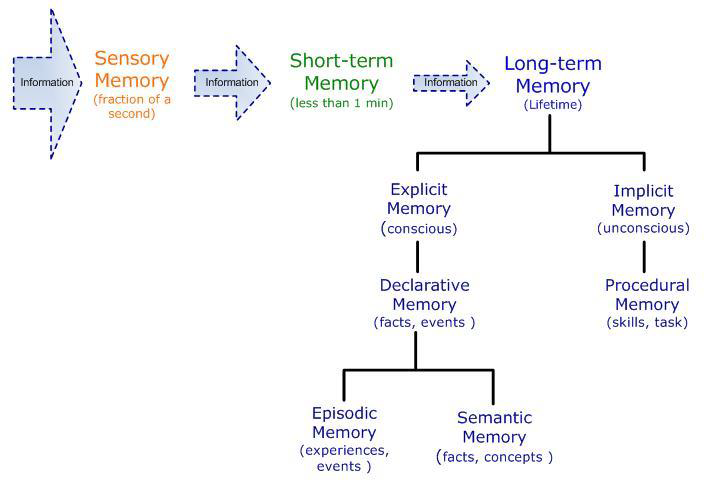
Working memory is the mental sketch pad we all use to manage and manipulate new understanding. It enables us to temporarily hold a piece of information whilst we work with another aspect of a problem and then retrieve it to complete the solution. Working memory relies on information that we have stored in long-term memory. This is information that we can readily recall because we have rehearsed it enough to store it without totally forgetting it. New learning often requires us to bring back some information we are familiar with from long-term memory and combine it with new information so that our learning can grow.
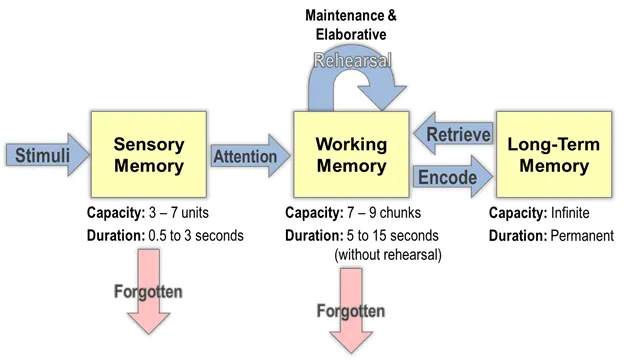
New information comes to us initially through the senses. Once we have given it attention, it enters our working memory so that we can use the information to develop our learning using retrieval from long-term memory. The main problem is that we only have a couple of seconds to attend to the sensory input and only about 15 seconds to utilize our working memory before the problem we are trying to solve is completely forgotten! This is true for all of us, not just for students with disabilities.
Long-Term memory breaks down into different retrieval sources that are basically either consciously learned or unconsciously acquired. The movements that naturally occur in early childhood are the unconscious underpinnings of our subsequent learning of number facts.

Types of Memory
We have memories of experiences and events that further support our growing understanding so that we can manipulate facts and events to build our knowledge base.
For students who have difficulty with movement and communication these natural building blocks are interfered with and the need for explicit rather than implicit learning becomes more vital.
Young-Leveridge (2011) argues that counting is not the only way for students to begin to develop numerical thinking. She suggests that subitizing, which involved recognising small numbers of items without the need to count them, as a quantification method through recognising patterns. In this approach concepts such as more and less than become more important than the actual numerical value when first encountering a quantity. By learning general principles of comparison children become more confident with applying number to something that they have learnt to recognise in a different way to linear counting. Of equal importance to numerical values are such mathematical concepts such as size, measure and shape. She goes on to suggest that an overemphasis on counting, while initially effective, may make it difficult for students to develop advanced math skills in areas such as fractions, proportions and multiplication.
Leuenbeerger et al (2024) suggest that non-counting strategies should be supported from the earliest stages of mathematics education, especially with students who have learning disabilities in the area. They maintain that frequent counting errors leads to difficulty with more mature mathematics understanding. Like Young-Leveridge, they advocate a more conceptual approach where an approach of grouping and quantity is appreciated.
Basic maths competence is seen as operating through three phases sequentially:
-
- Counting strategies such an object manipulation, using fingers etc
- Reasoning strategies which involve using known information to deduce answers.
- Mastery where the student has automatic recall of number facts.
It is important to note that students with physical and communication difficulties are often unable to experience phase one which might go some way to explaining why problems with number persist with this group.
Baroody goes on to explain that early operations are fact-retrieval skills, which we know the cohort of students we are referring to struggle with. He describes the fact-retrieval component of the brain as being separate from the conceptual and reasoning components of the brain. He goes on to suggest that learning number by rote requires more time and effort then recognising through establishing patterns and relationships. He argues that well connected factual knowledge is easier to retain than learning facts in isolation. He concludes that students who have difficulties mastering number should be provided with flexible options and routes through conceptual understanding and strategic mathematical teaching through purposeful instruction and guided inquiry.
Hargreaves et al (2025) identify a problem experienced by low-attaining students in that their motivation for learning becomes blocked by a sense of incompetency with subsequent negative impact on learning outcomes as students become focussed on their distress rather than in engaging in learning. This suggests that we need to focus on instruction that creates success rather than repeated failure.
The 2021 OFSTED review of mathematics identified three areas of mathematical knowledge as follows
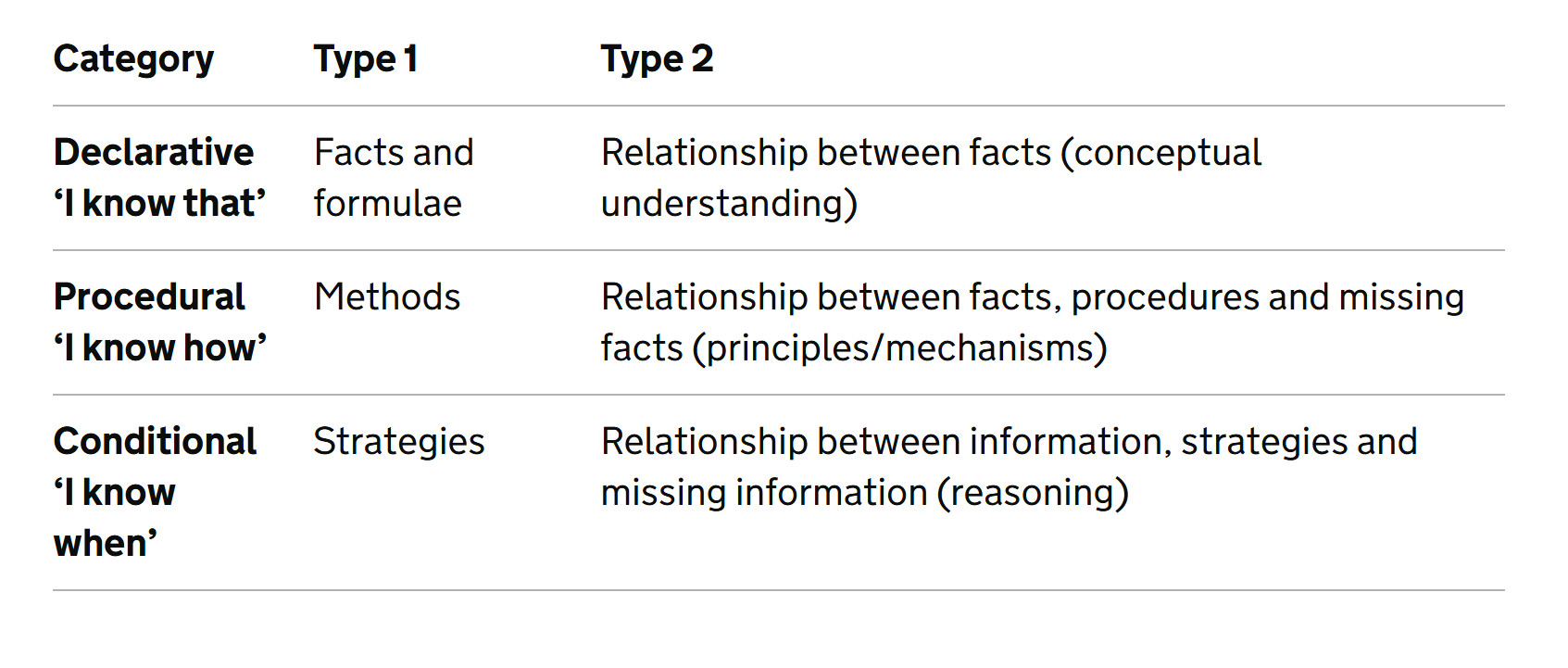
The evidence suggests that students who rely on AAC (Augmentative and Alternative Communication) may have better procedural and conditional knowledge than they do declarative knowledge. This may be because the latter places more demands on retrieval from long-term memory and manipulation in working memory whilst procedural and conditional knowledge are less reliant on recall and can more easily become automated, scaffolded and coached through guided practice. A missed fact can stall a whole problem whereas a student might guess, reason, or use supports to carry out a procedure or choose a strategy without needing full memory access. OFSTED recommend the sequencing of declarative and procedural knowledge together rather than in a linear fashion which makes declarative knowledge a precursor to procedural knowledge.
Familiarity with the facts helps with learning and understanding but familiarity with method helps to make associated facts firm and precise in the mind.
https://www.gov.uk/government/publications/research-review-series- mathematics/research-review-series-mathematics
Bailey et. Al. (2020) focussed on strengthening conceptual and procedural foundations of arithmetic. This involved delivering structured lessons emphasising deep understanding of number concepts (such as place value and the meaning of operations) in addition to rote procedures boosted arithmetic (declarative) outcomes. However, they found that gains faded unless long-term strategies of a similar nature were put in place. In addition to fluency drills the intervention supported engagement with procedural problem-solving tasks without time pressure.
Ncube and Luneta (2025) found that concept-based instruction (CBI) improved learner performance by promoting deeper understanding of underlying principles rather than rote memorisation. The intervention focused on developing conceptual understanding of the mathematics of functions, rather than basic numeracy operations, aiming to improve higher-level thinking across ideas.
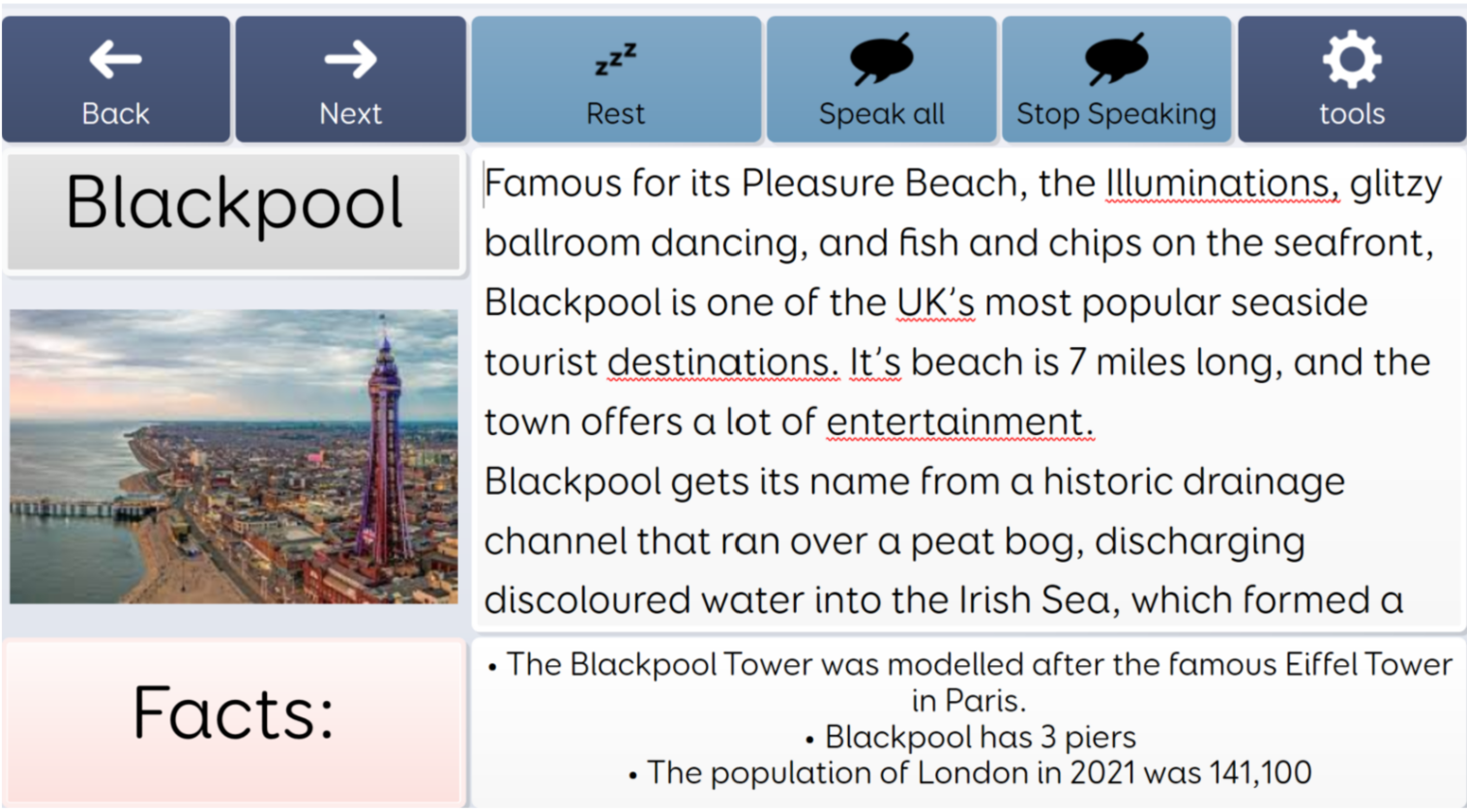
How can we support the cohort of students who have movement and communication difficulties?
By the nature of their physical difficulties this group of students are unable to develop their maths skills through early motor exploratory activity or from engaging with manipulatives. This suggests that we need a different approach to maths instruction for this group and that we must find a way to offer them these early learning routes in ways that are accessible to them.
Having repeatedly observed students failing to get beyond the numeral 10, and sometimes 5, using the traditional routes of counting and number bonds first, an alternative approach must be sought. Over the past few years, I have been working with many students in different ways, and I cannot prescribe a one-fits-all approach. It may help to look at a range of different approaches and how they might help or hinder the development of maths skills.
In the following table the AAC student refers to students who have physical and communication difficulties:
| Approach | Advantages for allstudents | Disadvantage s for allstudents | Implications for disabled/AACstudents |
| Mastery Model Description: Students must fully understand a concept before moving on. | Promotes deep learning and reduces gaps in understanding. | Difficult to maintain focus in a class of students who are at different levels of mastery. | AAC students rarely learn in a linear fashion so may be impeded by a method that required skills to be built in a prescribed way. |
| Inquiry-Based Learning Description: Students explore and discover mathematical ideas through guided investigation. | Students explore and discover mathematical ideas through guided investigation. | Relies on a high level of teacher skill in terms of student needs and individualisation. Students need to be motivated. | AAC students will often lack the prerequisite skills for independent investigation because they do not have the technology and/or support to be able to develop their investigative skills. |
| Direct Instruction Description: Teacher-led, structured lessons with clear objectives and practice. | Efficient for skill acquisition and procedural fluency provided the student is able to converge with the teaching process. | Relies on the teacher having regular checks of progress through testing or some othermechanism. Not easy to individualise learning needs. | The AAC student could quickly be left behind because the huge amount of differentiation an dadaptive teaching required may be difficult to achieve in a busy classroom environment. |
| Socratic Method Description: Uses questioning to stimulate critical thinking and uncover understanding. | Encourages deep reasoning and dialogue. | Requires significant confidence on the part of students and teachers.Scaffolds and prompts will be important. | The AAC student can benefit from this approach provided they have appropriate prompts and scaffolds (such as multiple-choice options) so that they can consider choices rather than having to‘think laterally’. |
| Cognitive Apprenticeship Description: Learners observe expert thinking, then practice with guidance. | Makes thinking visible and supports skill development. | Requires guidance for students to be able to progress. | The AAC student is really supported by this approach as it is individualised and the student benefits from continual guidance. |
| Spiral Curriculum Description: Concepts are revisited at increasing levels of complexity | Students revisit concepts regularly at increasing levels of difficulty so that their understanding deepens. | May feel repetitive for student who grasp concepts quickly. | AAC students can benefit from the repetition with the variety of incremental levels of difficulty being introduced. |
| Network Model Description:Concepts are interconnected in a web-like structure. | Encourages flexible thinking and deep understanding through relationship between ideas. | Students may become lost in a web of inter connections that might not be intuitive for them. | AAC students can benefit from drawing on their non-counting strengths to support the development of counting skills. |
| Concrete·Pictori al·Abstract (CPA) Description: Progresses from hands-on manipulatives to visual representations to symbolic notation. | Supports conceptual development and scaffolds learning. | Assumes that all students follow the same trajectory from concrete to pictorial to symbolic. | AAC students generally fall at the first post with this approach as they are often unable to engage with the early, hands-on stage. |
| Problem-Based Learning (PBL) Description: Learning is driven by solving real- world or complex problems. | Encourages application af knowledge through real world situations and collaborative learning. | Can be difficult to extract the mathematics needed to solve the real- world problem. | AAC students can benefit from being able to apply mathematical principles to real world problems BUT this approach often involves several stages which the AAC student needs to be supported through and able to refer to as they proceed through the problem-solving process. |
| Constructivist Model Description: Learners build their own understanding through experience and reflection. | Learners build their own understanding through experience and reflection. | Very dependent on the quality and depth of the learner’s day- to-dayexperiences. | The AAC student may be left floundering by this approach because they may not have the same level of world experience as their peers and can then quickly be left behind.Building experiences is essential if this approach is to be used. |
From this analysis the approaches most suited to the students who rely on AAC are:
-
- The Socratic method provided appropriate scaffolds are in place
-
- The Cognitive Apprenticeship approach provided appropriate scaffolds and models are in place.
-
- The Spiral Curriculum which enables repetition at spaced intervals with increments of new learning within already familiar approaches.
-
- The Network model which enables students to use their existing strengths to develop further skill and to make connections.
-
- The Problem-based learning model which connects mathematical principles to real world situations.
None of these models place the skill developments of counting and number bonds as prerequisites to learning. Instead, they foster the development of more generalised knowledge such as:
-
- Knowing which operation you need to use.
-
- Being able to discern patterns.
-
- Being able to orient in space and identify shape and, measure.
-
- Having an ability to discern quantity.
-
- Being able to connect ideas.
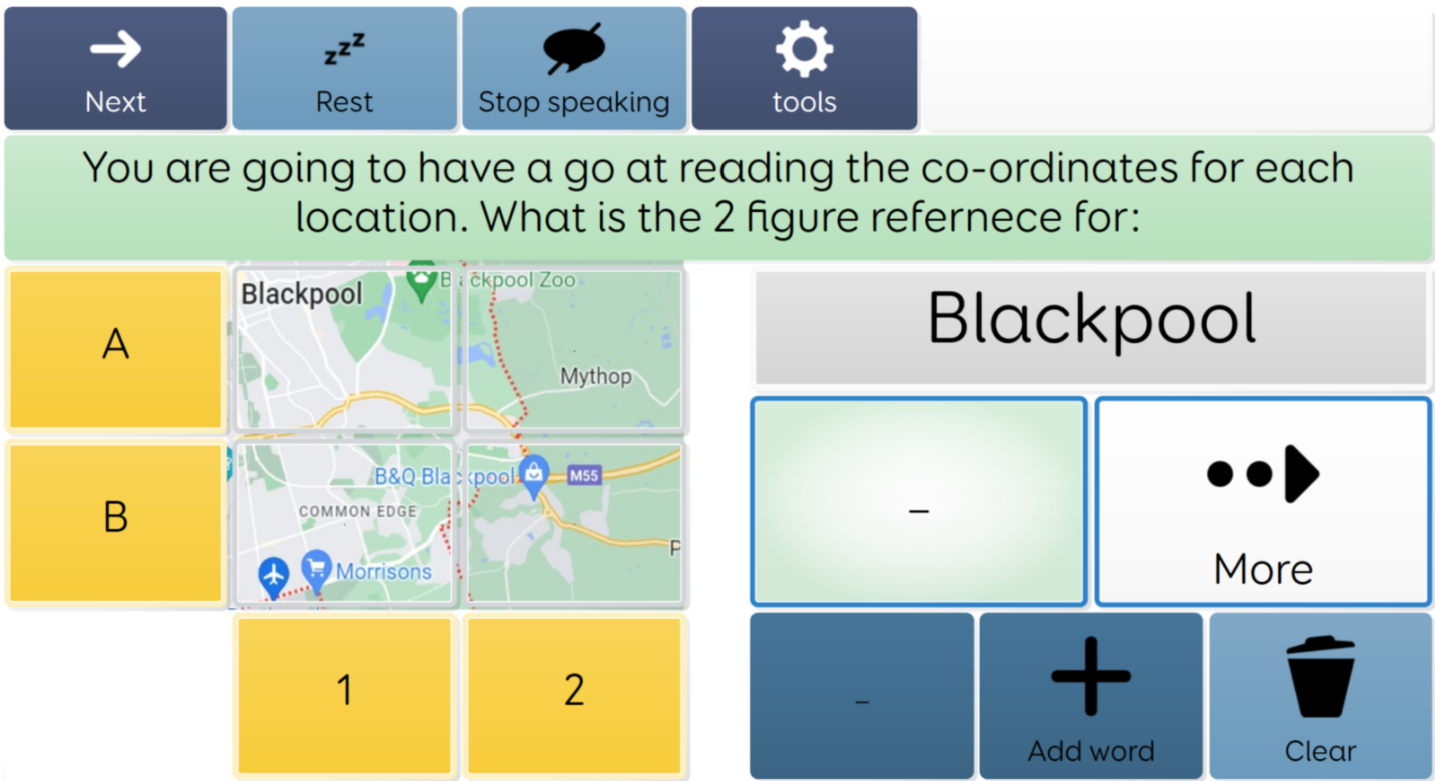
Potential Solutions for students who rely on AAC and/or have physical and communication difficulties
In the following example the student can use eye gaze, switches or other access to technology to investigate number and demonstrate understanding. If they need an answer it is there. The blue number plus any white number equals the blue number above the white number. This gives that AAC student the opportunity to practice skills repeatedly but in a variety of settings allowing generalisation and skills building to take place.
The most important point about these activities is that they allow the student to work independently without too much physical effort and in the most time effective way. Monei and Pedro (2017) confirm that strategies that reduce working memory effort are the most effective. With a student population that relies on assistive technology to achieve learning it is essential that the design of programs incorporate ease of access to preserve working memory as well as supporting independent access.
Independent working does not mean unsupported working. The student still needs to be scaffolded by a more knowledgeable other be it their teacher, parent, sibling, friend or teaching assistant.
In the following example the concept of plus 2 is being demonstrated so that the AAC student can practice that skill:
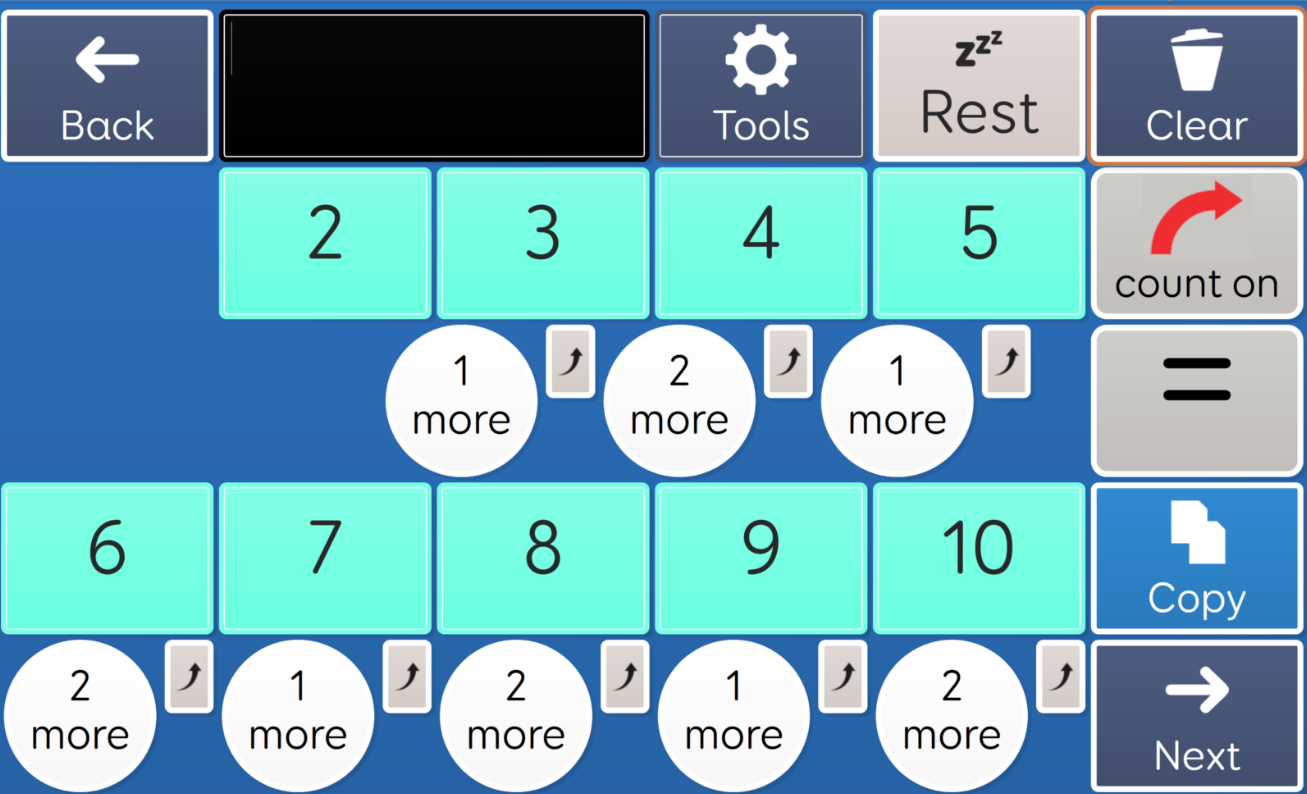
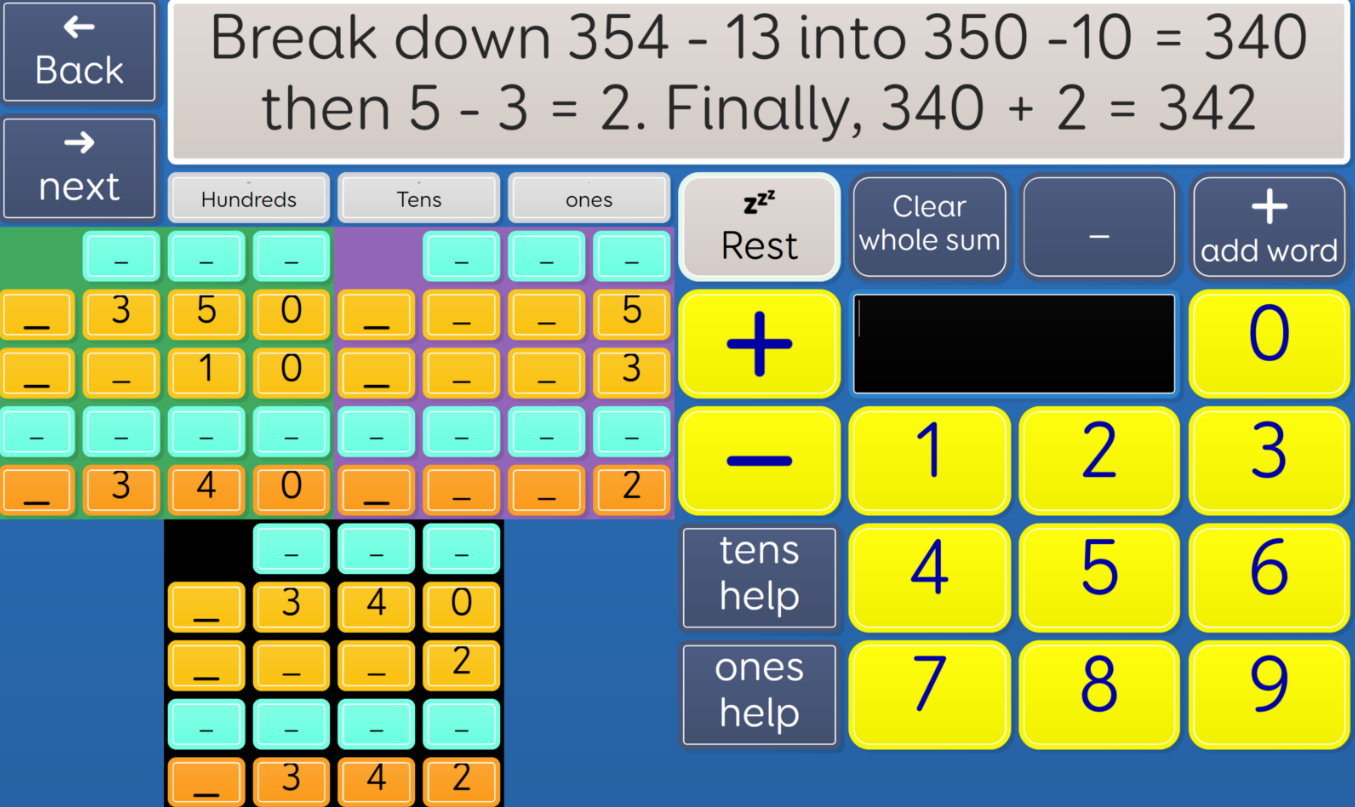
Hopkins et al (2022) found that many students use min-counting (counting on from the smallest number) but they maintain that this strategy is less effective than retrieval (automatic recall). A third group of students used decomposition which involves breaking complex problems down into simpler steps such as 345 – 12 = 345-10 =335 -2 = 333. Since retrieval is a difficult skill for AAC users to master (on account the time and repetition needed), decomposition may present a more workable solution. However, the breaking down of steps, in itself, could compromise working memory.
In the following example the steps are kept on the same page, but the cells end up being very small so that access may be compromised.
A reasonable adjustment for a student that still struggles with counting is to provide the following supports:
 |
 |
I have often been challenged in the past on recommending this kind of support as it is seen as cheating because the students are being given the answer. This is far from the truth. They still must understand the rules by which the support operates, and they then must select the correct support. What this also gives them is the repeated exposure that they need as a scaffold on the way to independent mental operations. It is vital that you teach before you test.

Constant checking to see if a student understands can be undermining, especially for disabled students. Valuable teaching time can be wasted with testing something that has not yet been sufficiently modelled and scaffolded. Unless you have first modelled (shown the student how a maths problem needs to be solved) and then scaffolded learning (given the student the problem but then given them hints to be able to solve the problem), you should not be testing.
Gervasoni (n.d) identifies five key skills that lead to confidence with number as follows:
1. Rote counting: Rote counts the number sequence to at least 20.
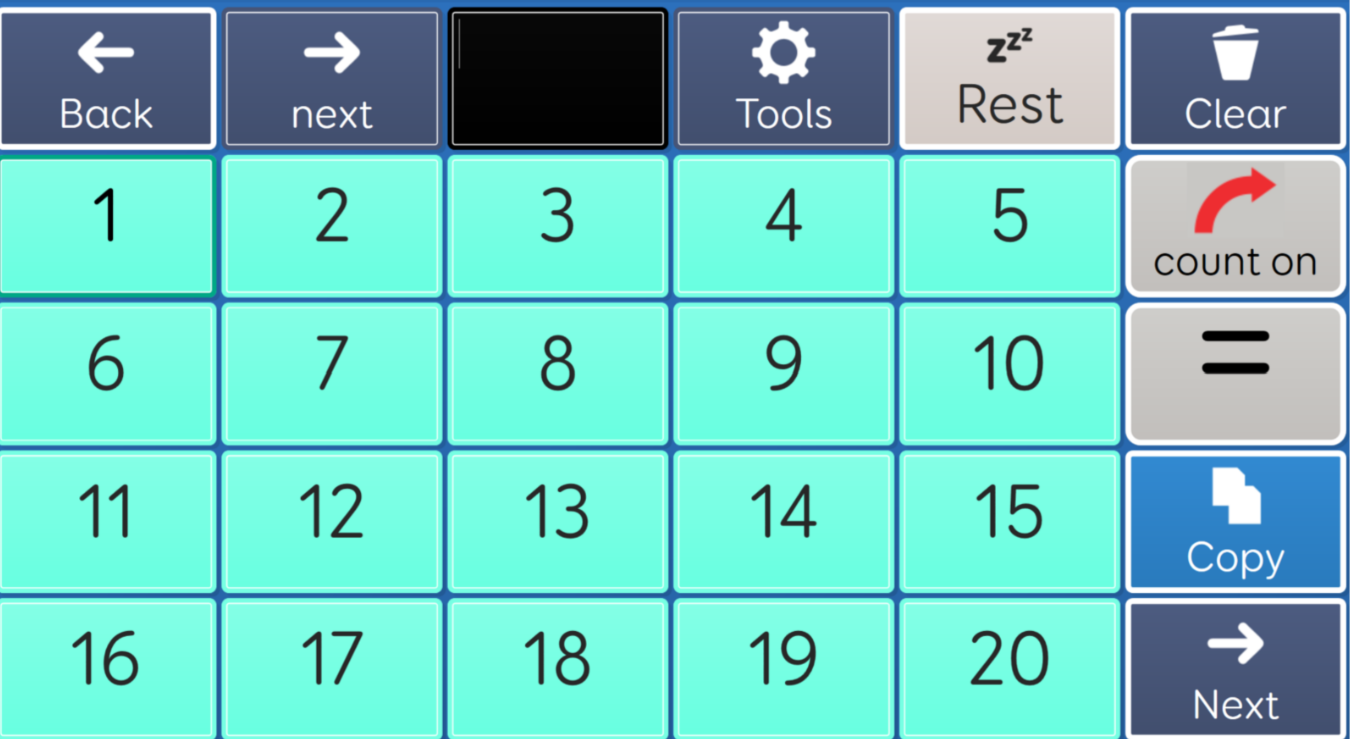
-
- Counting collections: Confidently counts a collection of around 20 objects.
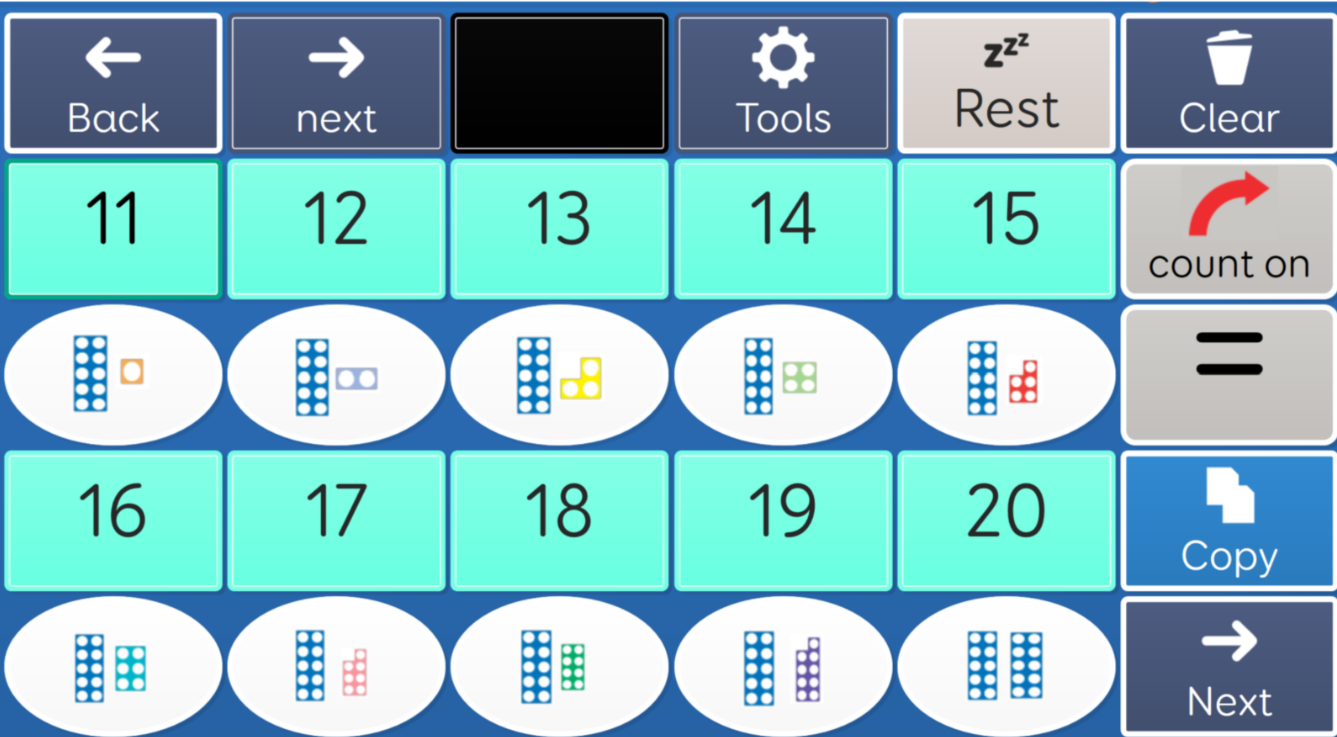
-
- Counts forwards and backwards from various starting points between 1 and 100; knows numbers before and after a given number.
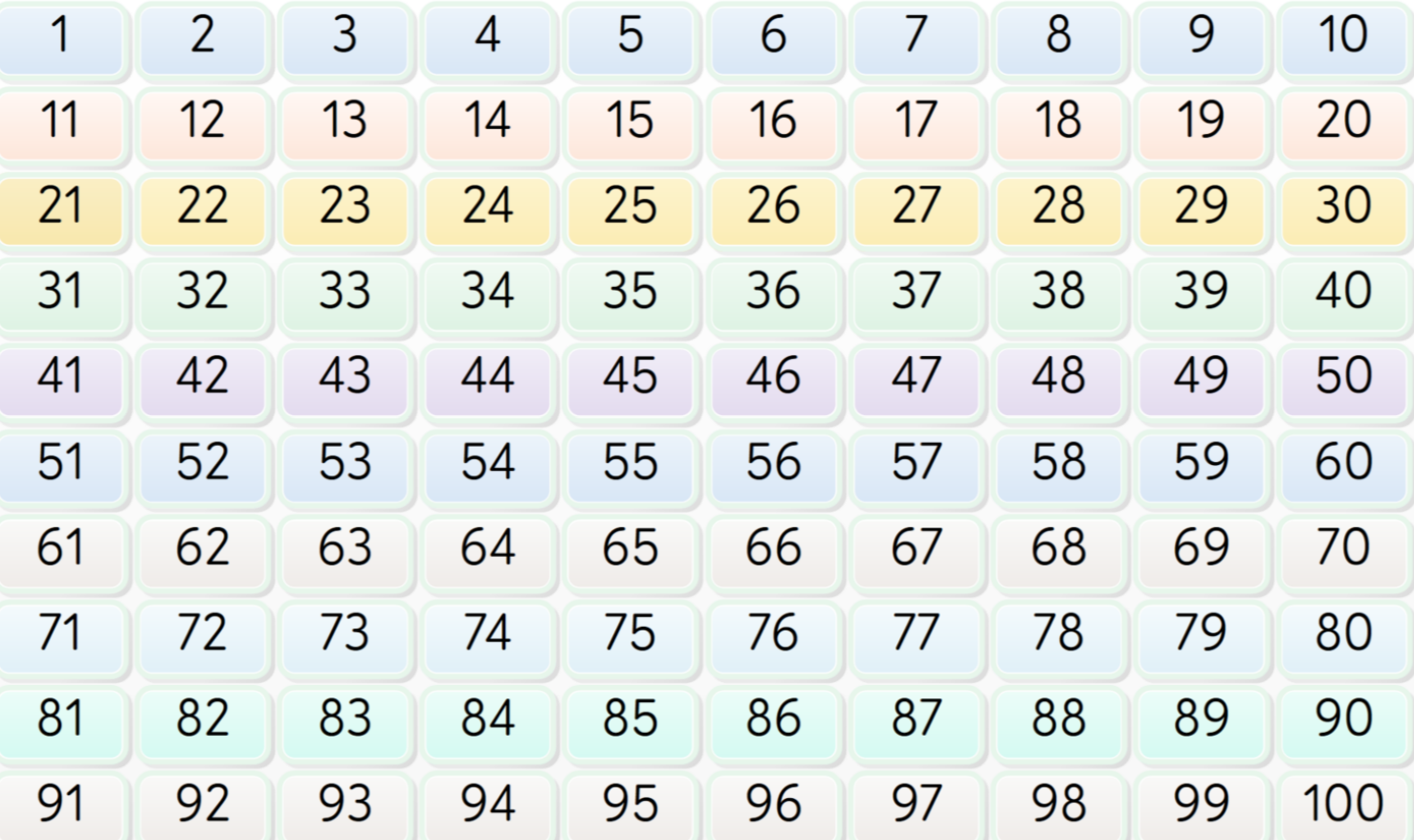
-
- Counting from 0 by 2s, 5s, and 10s: Can count from 0 by 2s, 5s, and 10s to a given target.
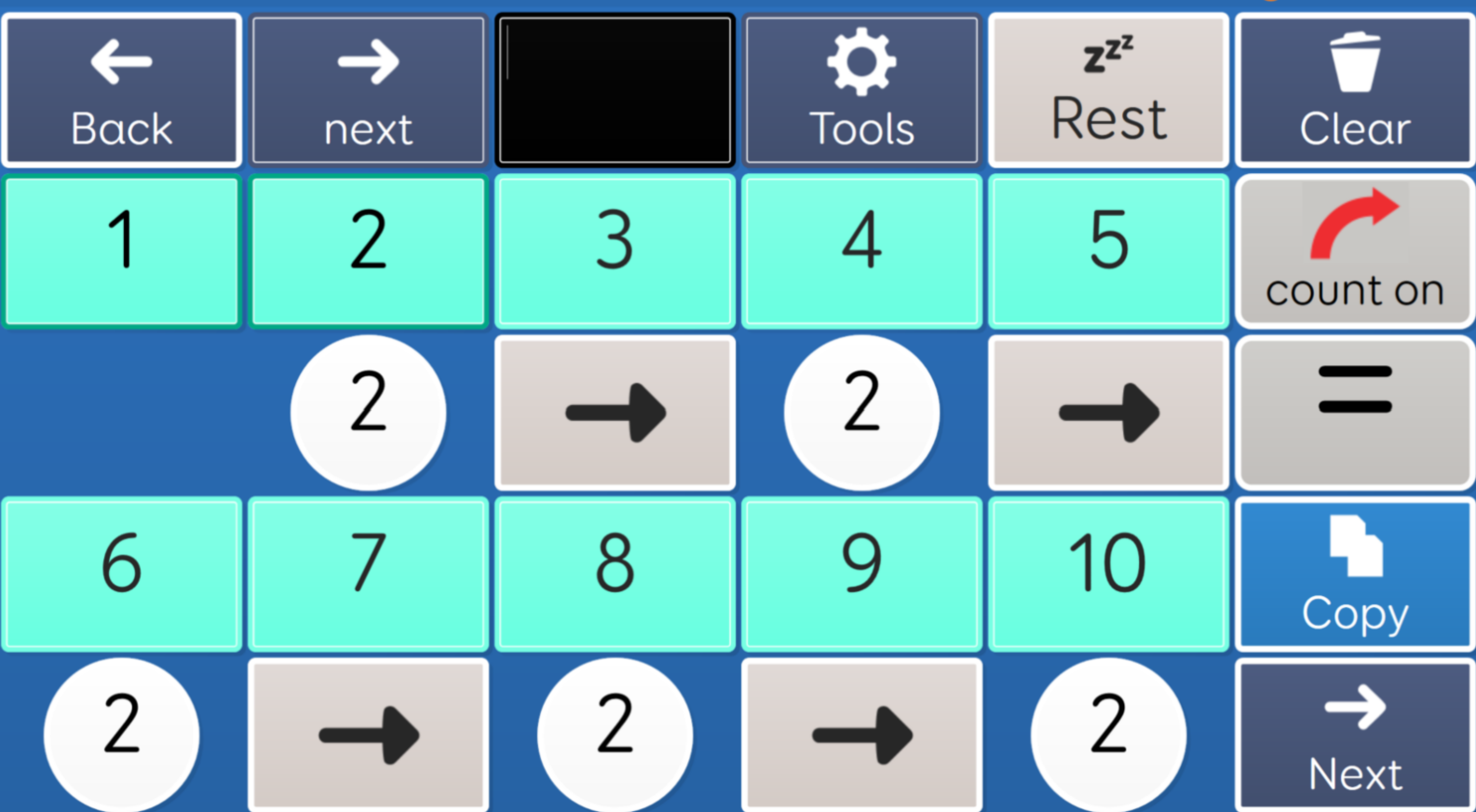
-
- Counting from x (where x>0) by 2s, 5s, and 10s: Can count from x by 2s, 5s, and 10s to a given target.
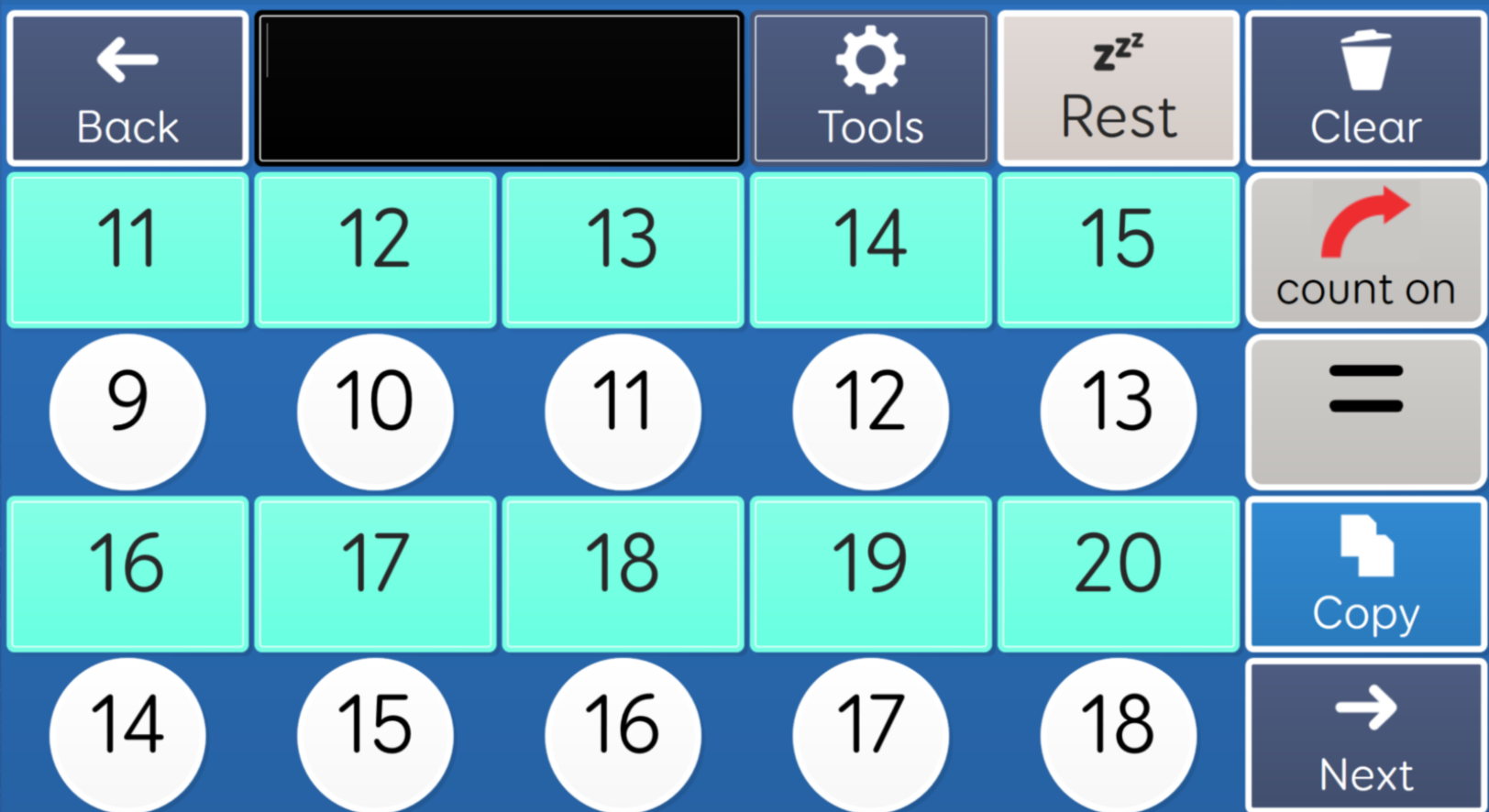
-
- Extending and Applying: Can count from a non-zero starting point by any single digit number, and can apply counting skills in practical tasks”
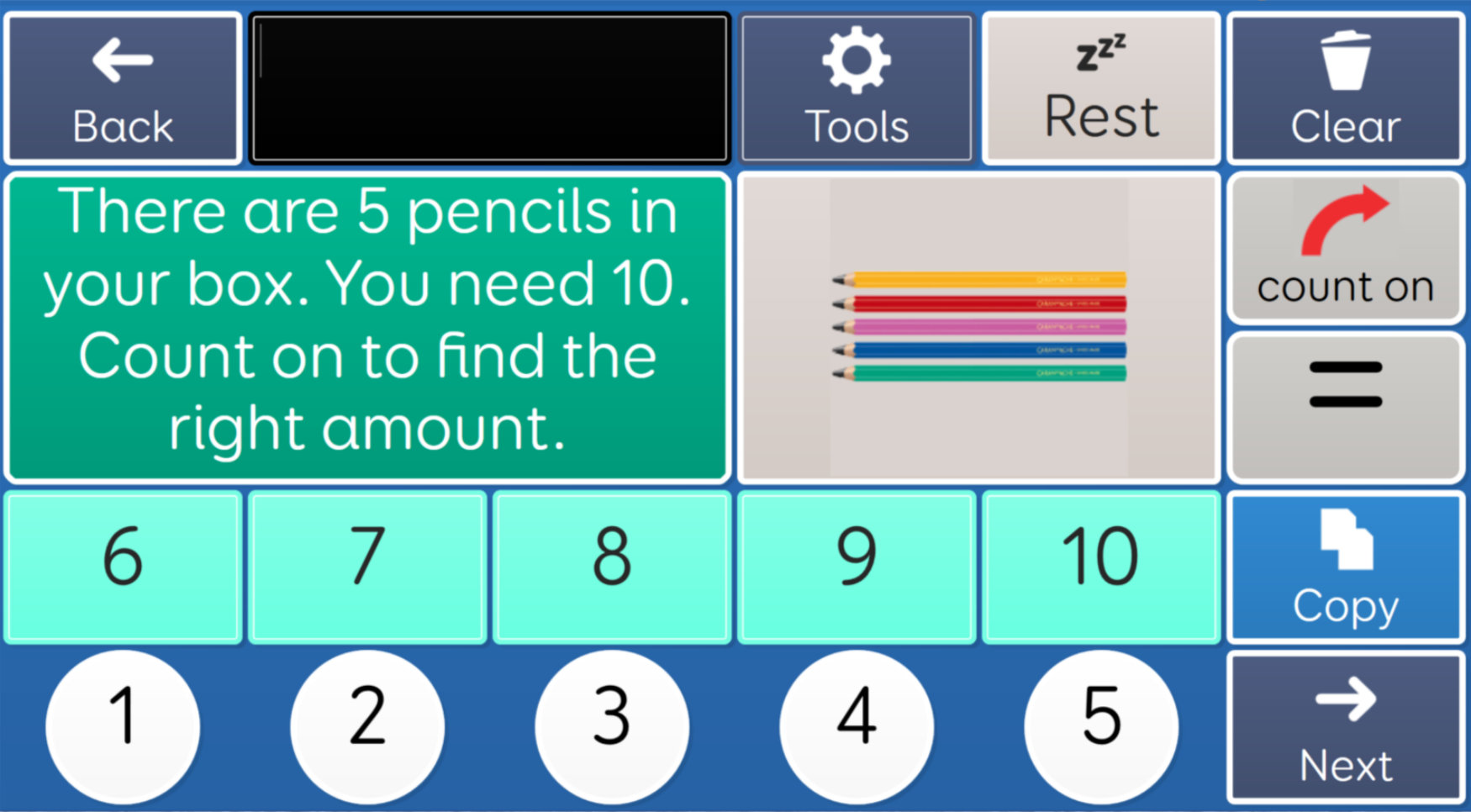
Although repetition is vital it is much more effective if it is carried out with variety. Counting the same 5 things every day does not enable generalisation to all things that are 51. Repetition with variety is encapsulated in several approaches including: mastery, scaffolding, spiral, and spacing. Let your variety include the introduction of more complex concepts than those that already appear to be grasped. For example, even if you feel a student can only count to 3, teach them to 10. 20 and beyond. This will give them a sense of progression and avoid students glossing over through boredom and lack of motivation. This is an example of teaching the same understanding in different ways:
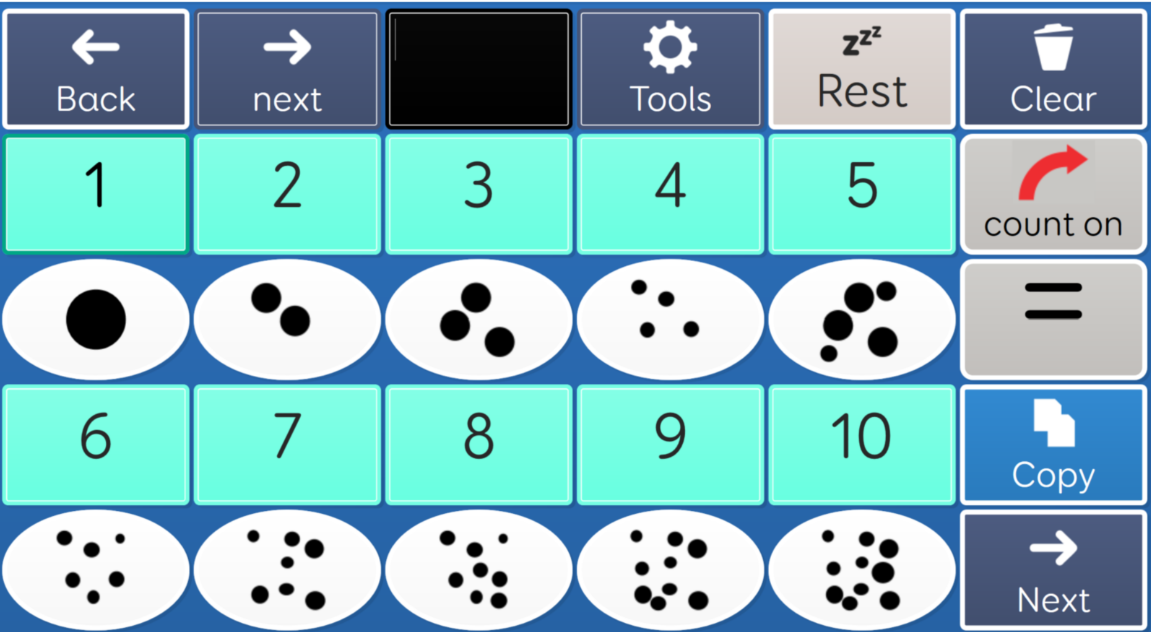 |
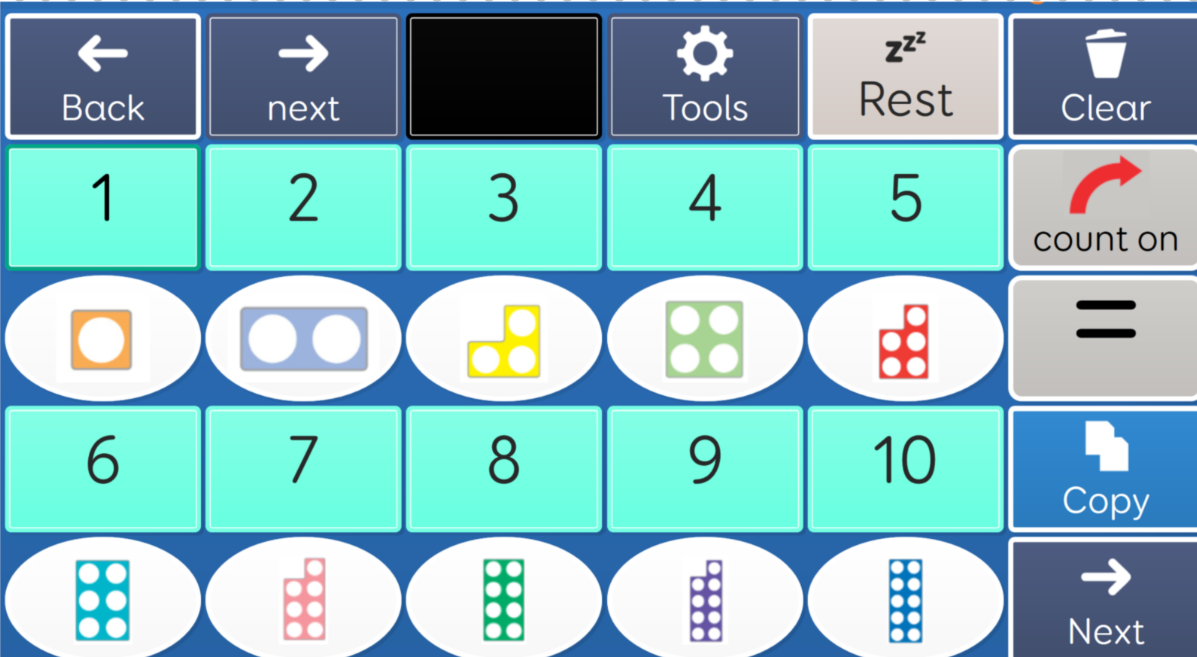 |
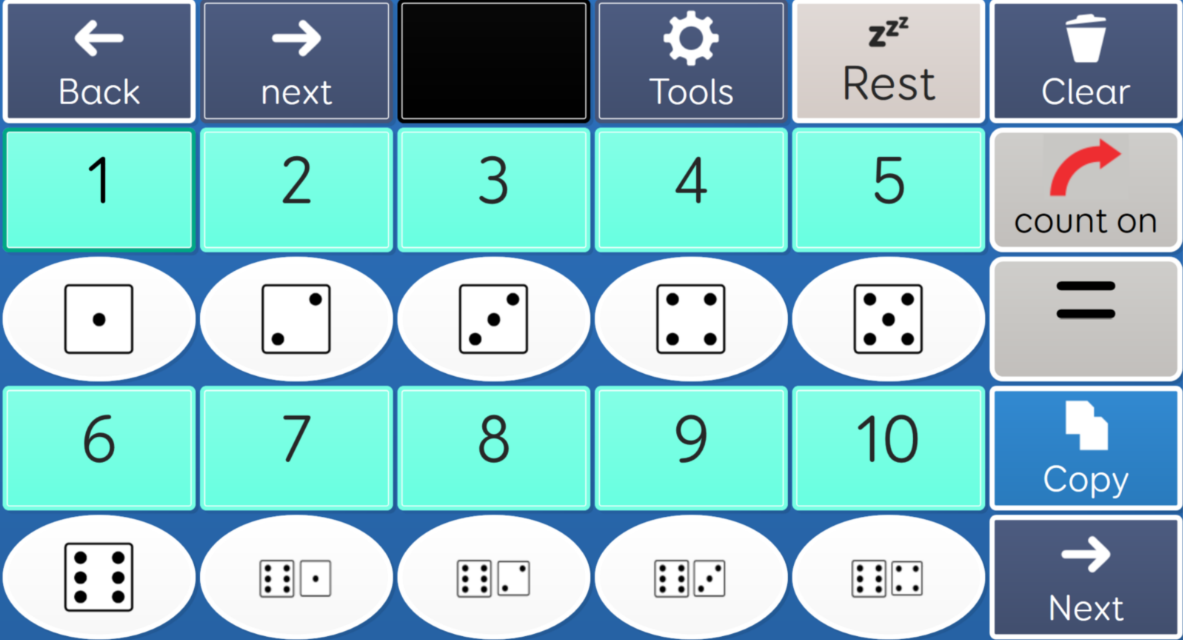 |
Explicit instruction in the strategies needed to complete these tasks without the distraction of contextualisation may be helpful for this cohort of students. However, if the student is showing no improvement an alternative approach may be required and should be integral to all teaching and learning for all students.
Rosenshine (2012) identifies 12 principles of instruction that should be considered as follows:
-
- Review previous learning before going on to new learning.
- Present new material in small steps with student practice after each step.
- Ask many questions so that students experience guided practice.
- Provide models (worked examples)
- Guide students practice with questioning, providing additional information, explaining each step, correcting errors and supporting students in working out problems.
- Check for student understanding and reteach or reframe if necessary.
- Obtain a high success rate. Aim for 80% success rate.
- Provide scaffolds for difficult tasks. These are temporary supports that are gradually withdrawn as the student gains in confidence and ability.
- Require and monitor independent practice.
- Engage students in weekly and monthly review (spaced learning)
Spaced learning has been found to be a productive way to embed learning but has yet to be fully incorporated into curriculum delivery in the UK. It involves returning to learning several times after a set time. In each return the time is longer.
https://www.tes.com/magazine/tes-explains/what-spaced-learning
In our desire to ensure that a student has grasped basic understanding before we move them on to more complex, reasoning based learning we may be further reducing the learning potential of students who may need another route into learning than is traditionally achieved through practice and rote learning. Spaced learning may be another route to grounded learning.
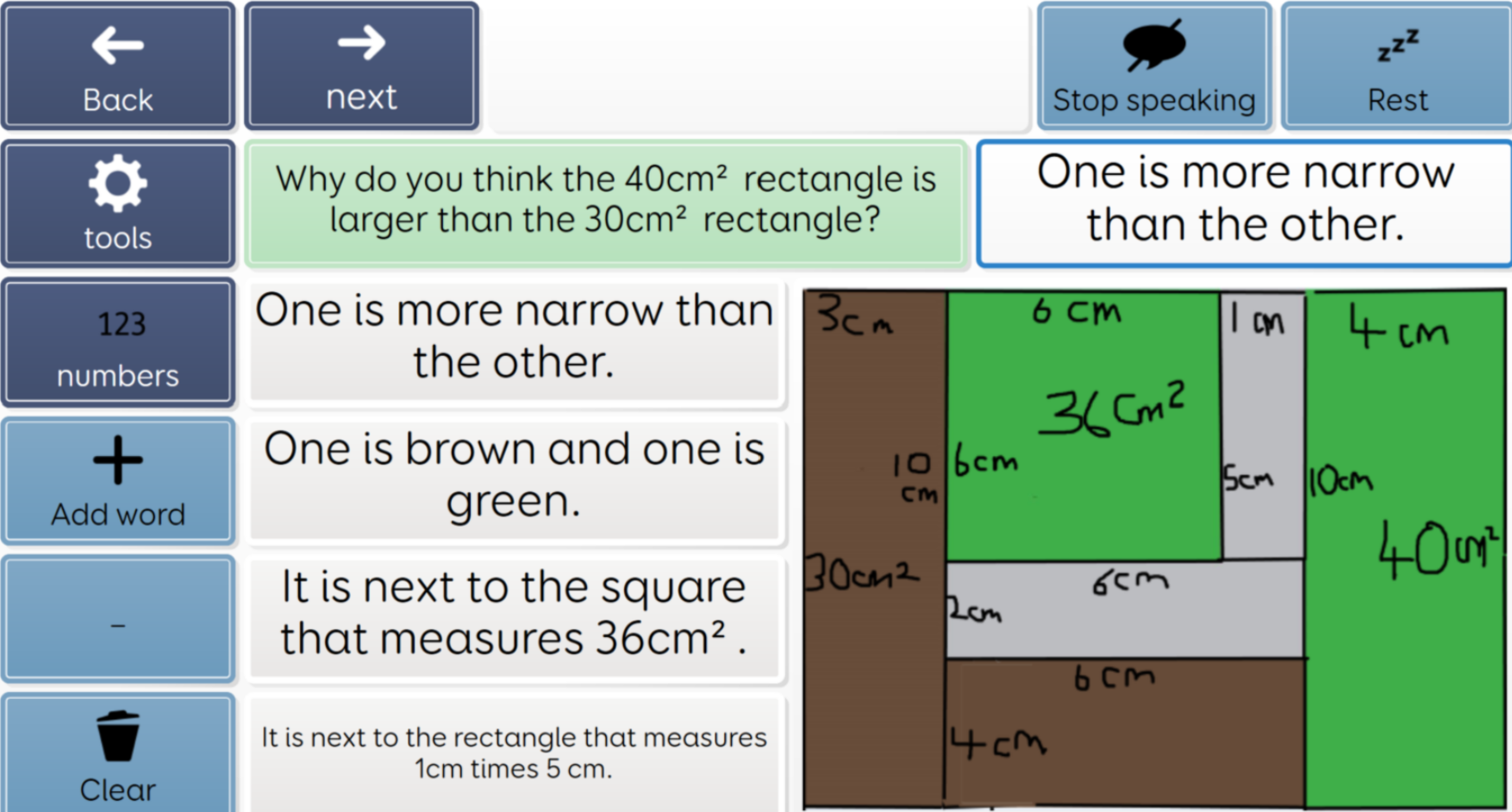
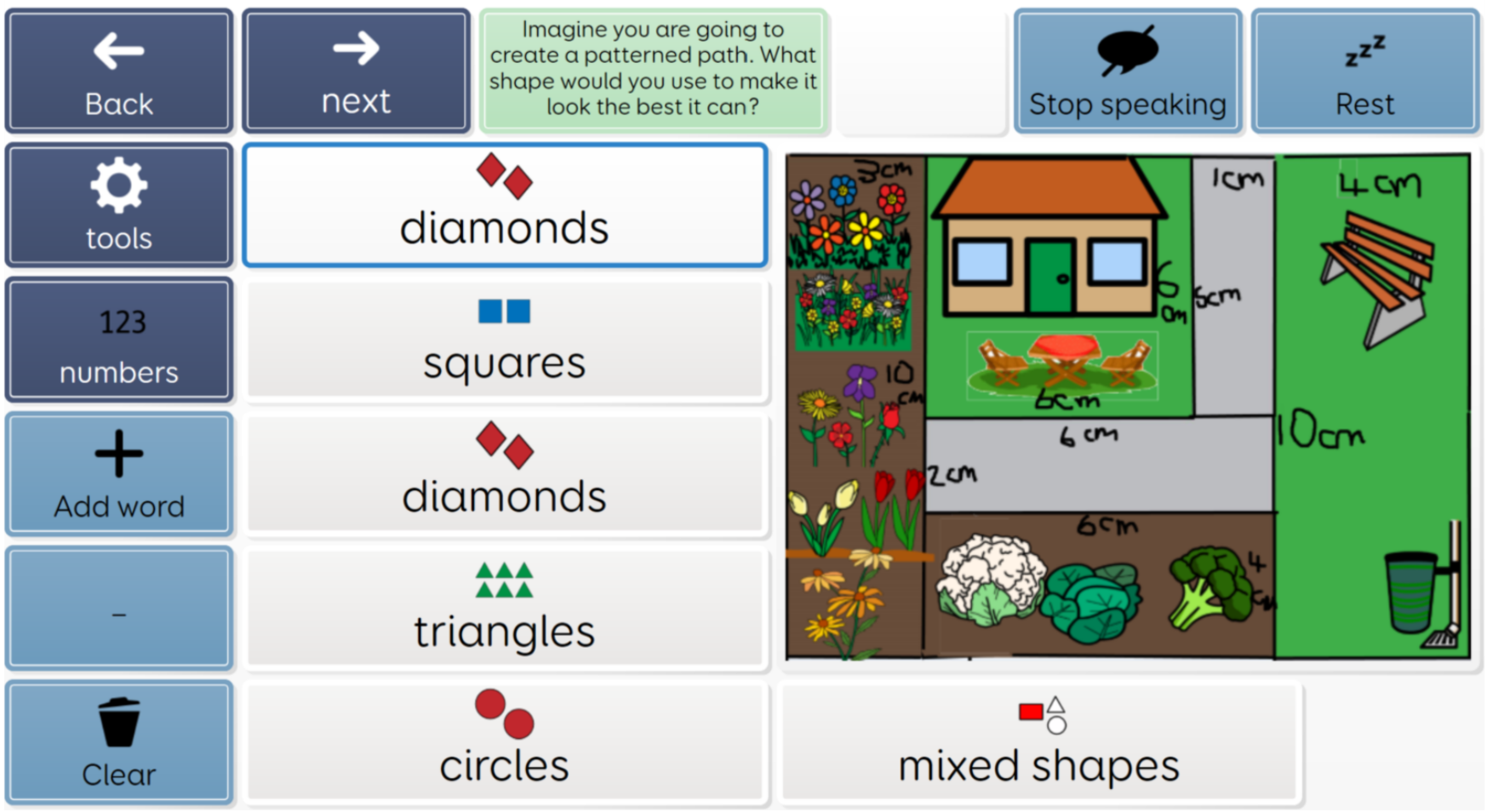
CandLE is developing a ‘thinking skills’ maths program which exposes students to number in incidental ways and always with an application based in real world experiences as well as supporting the understanding of concepts. This is an example of consolidating some previous work on shapes and introducing size and measure with number being incidentally used (repetition with variety and spaced learning).
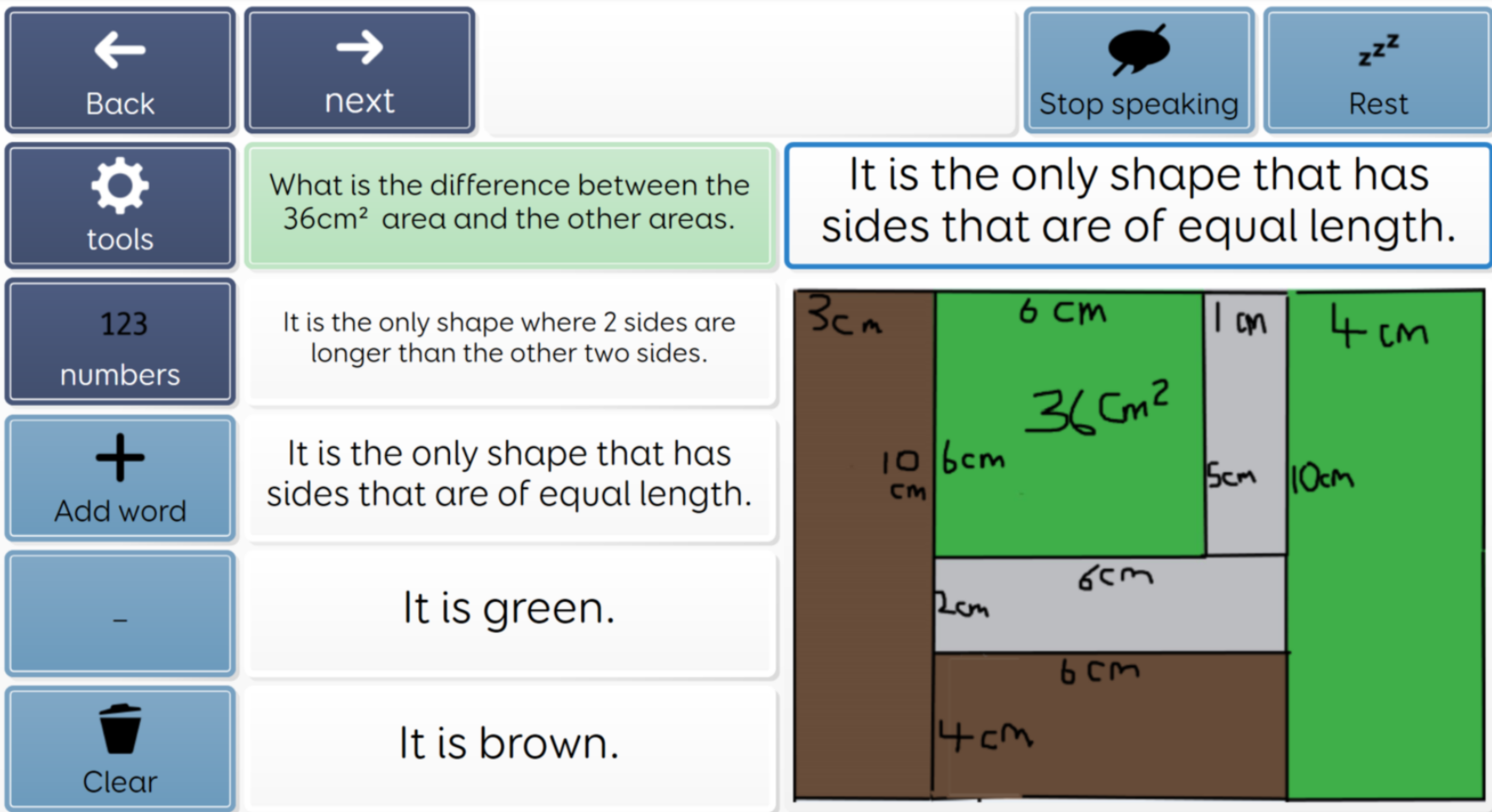 |
 |
 |
 |
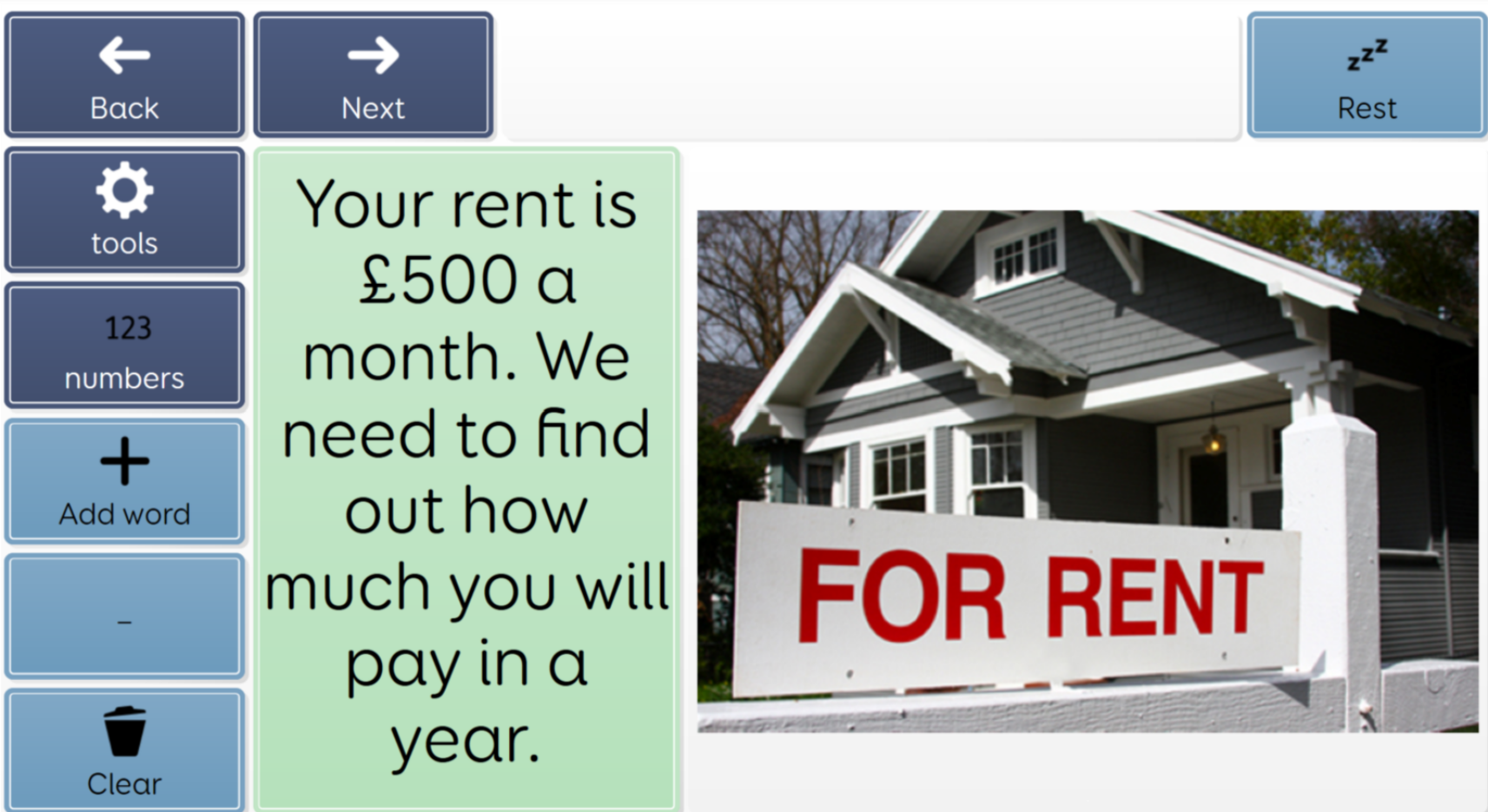
Using a story about a family that is buying a house, creating a garden then going on holiday, we contextualise maths into a real-world situation. We don’t expect the student to use recall or retrieval. We give them a number square or a calculator for that but we do want them to know how to work out the answer to the problem :
 |
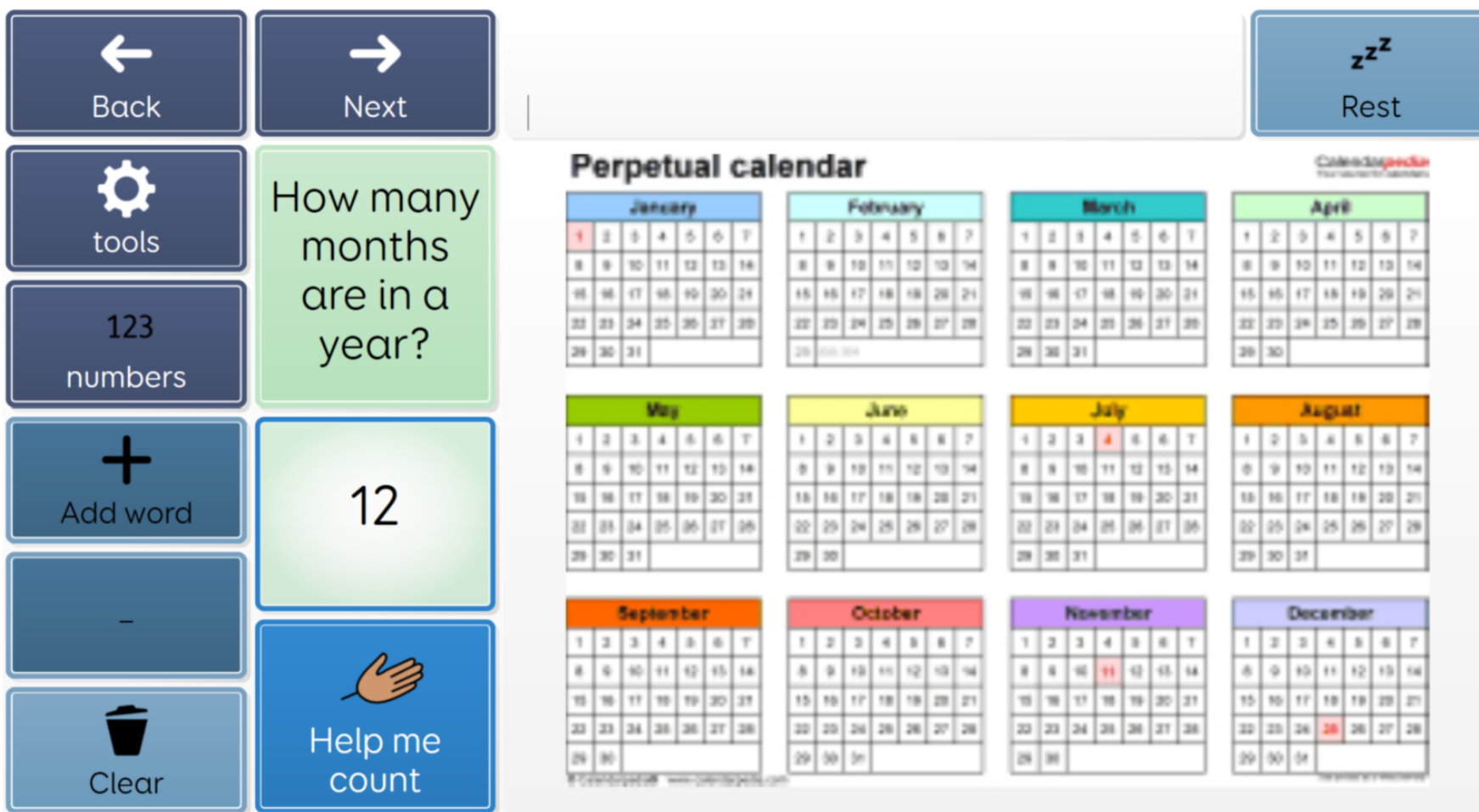 |
 |
 |
 |
Here we are recapping measure before going on to use number in a context using estimation and developing world knowledge:
 |
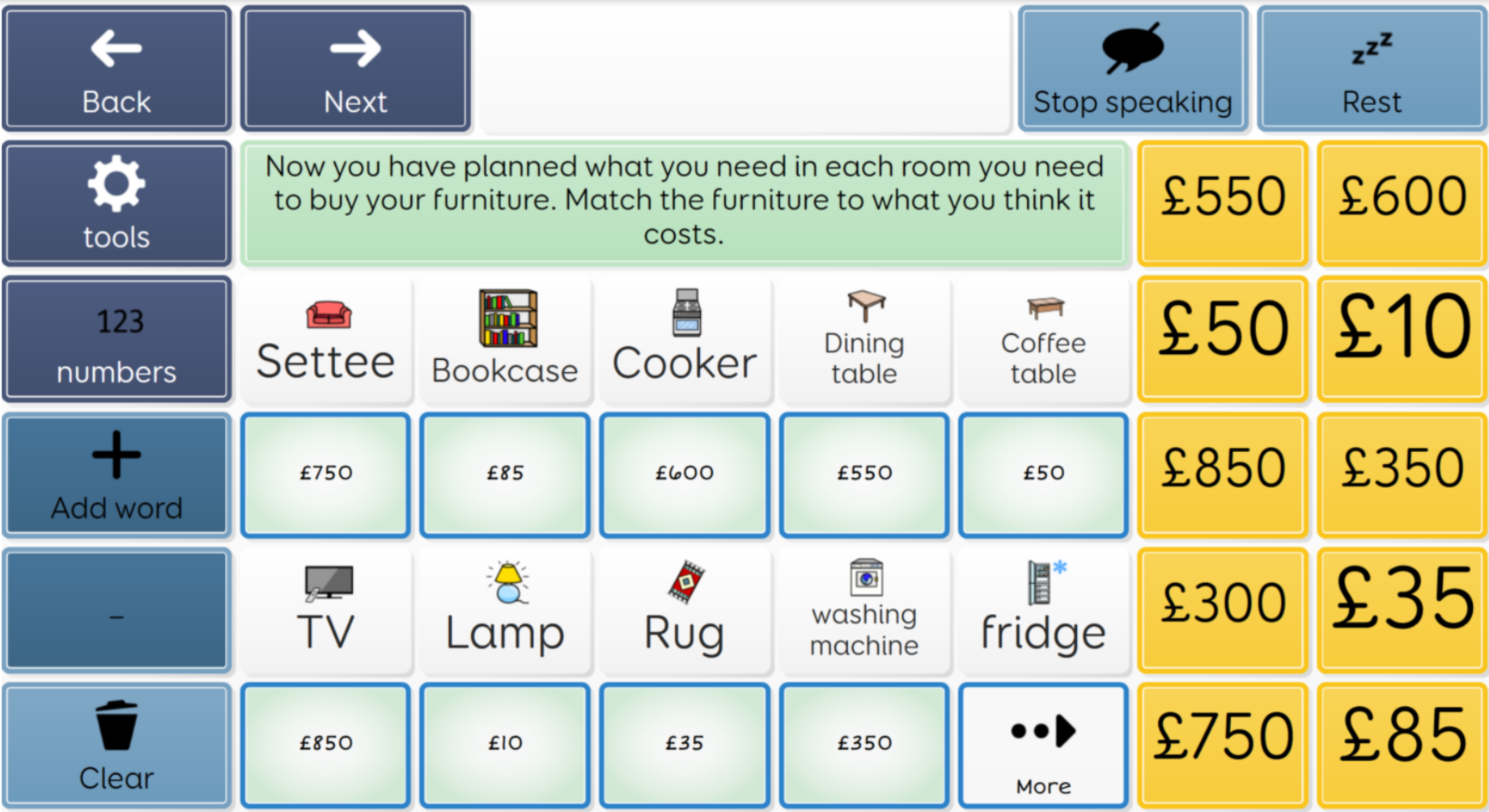 |
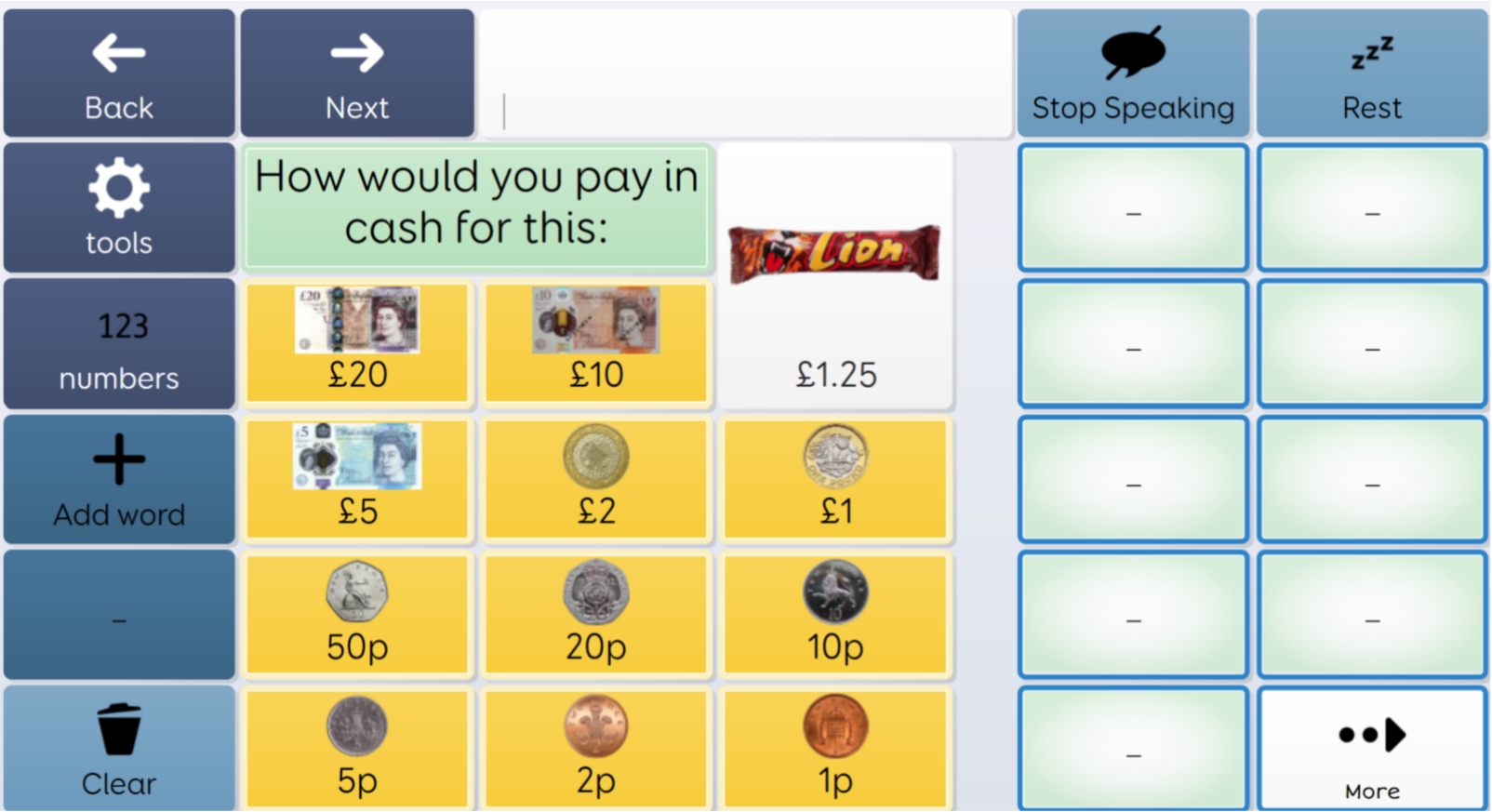 |
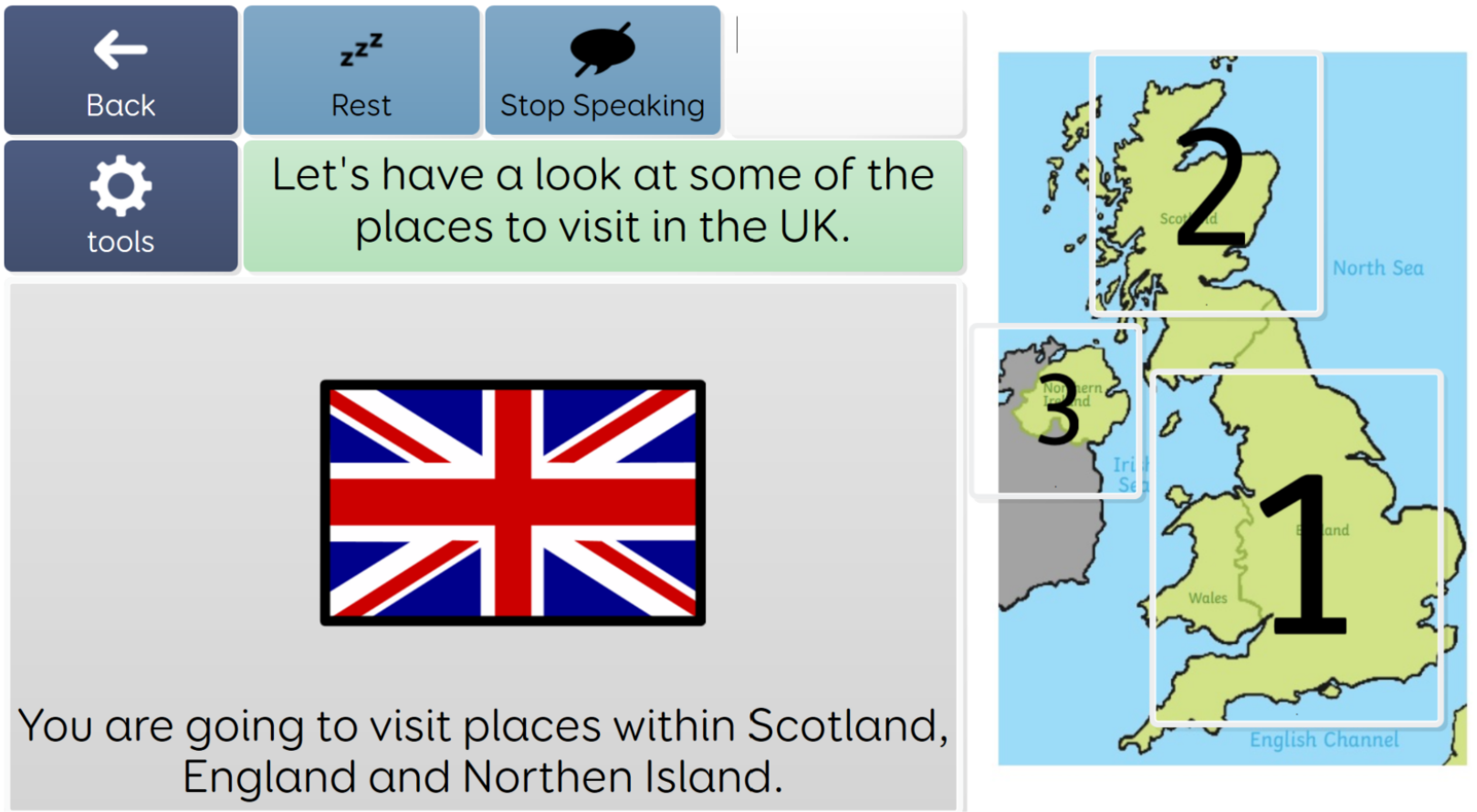 |
 |
 |
 |
 |
All the maths problems shown have been completed by students who still struggle with counting to 10 but, by working with broader maths concepts they are beginning to consolidate basic numeracy incidentally.
Researchers at Nottingham University found that improving children’s multiplication fact recall through retrieval practice doesn’t equate to improving their ability to use the multiplication facts they know. Children who can recall a multiplication fact such as 5 x 7 = 35, may not be able to use this fact to solve a problem such as “Tara has 7 books. Ravi has 4 times as many. How many books do they have together”. (Guy et al 2025)
The expectation in the UK is that students should know their times tables by the end of year 4. Given that students with physical and communication difficulty may take up to six times longer than their non-disabled peers to acquire knowledge that needs to be rote learnt this cohort could be in their mid-20’s before this is accomplished. The length of extra time calculation is based on CandLE findings when preparing for exams and timing student responses. By extension it can be inferred that it could also take a protracted length of time to achieve number bonds at a basic level. This is even if the students are not further disadvantaged by the fact that taking longer will have a negative impact on working memory and may make rote learning an even lengthier process if it is achievable at all.
So, let’s move on beyond basic counting and number fact recall and support students to experience mathematical concepts in different ways. Allow them to use calculators, number lines, number squares and multiplication squares to get over the counting and fact recall hurdle. Instead, let them focus on how the problem should be managed.
References
Bailey, D. H., Fuchs, L. S., Gilbert, J. K., Geary, D. C., C Fuchs, D. (2020). Prevention: Necessary But Insufficient? A 2-Year Follow-Up of an Effective First-Grade Mathematics Intervention. Child Development, S1(2), 382–400. https://doi.org/10.1111/cdev.13175
Baroody, A.J. (2006) ‘Why children have difficulties mastering the basic number combinations and how to help them’, Teaching Children Mathematics, 13(1), pp. 22–31.
Critten, V., Campbell, E., Farran, E., C Messer, D. (2018). Visual perception, visual-spatial cognition and mathematics: Associations and predictions in children with cerebral palsy. Research in Developmental Disabilities, 80, 180–191. https://doi.org/10.1016/j.ridd.2018.06.007
Development of early numeracy performance in children with cerebral palsy: The influence of cognitive and motor factors. (2015). https://hdl.handle.net/2066/140585
Developmental Disabilities, 5c(6), 442–457. https://doi.org/10.1352/1934- 9556-56.6.442
Flores, P., Coelho, E., Mourão-Carvalhal, M. I., C Forte, P. (2023). Association between motor and math skills in preschool children with typical development: Systematic review. In Frontiers in Psychology (Vol. 14). Frontiers Media S.A. https://doi.org/10.3389/fpsyg.2023.1105391
Hargreaves, E., Quick, L. and Buchanan, D. (2025) ‘“This is too boring”: a life-history approach to primary pupils’ distress and lack of motivation for school-work’, Pastoral Care in Education, pp. 1–19.
doi: 10.1080/02643944.2025.2454650
Gervasoni, A. (n.d.). KEY TRANSITIONS IN COUNTING DEVELOPMENT FOR YOUNG CHILDREN WHO EXPERIENCE DIFFICULTY.
Guy, N., Cragg, L. C Gilmore, C., 2025. Learning, using and applying multiplication facts: Insights from research. Chartered College of Teaching, 19 May [online]. Available at: https://my.chartered.college/impact_article/learning-using-and-applying- multiplication-facts-insights-from-research/ [Accessed 1 Aug. 2025].
Sweller, J., Ayres, P., C Kalyuga, S. (2011). Cognitive Load Theory. Springer.
→ See Chapter 4: Redundancy Effect.
Leuenberger, D., Diener, M., Wehren-Müller, M., Hofmann-Villiger, A., Vogt, F., C Moser Opitz, E. (2024). Fostering Computation Competence with
Non-Counting Strategies and Conceptual Subitizing in Grade 1: An Intervention Study in Inclusive Classrooms. Journal Fur Mathematik- Didaktik, 45(2). https://doi.org/10.1007/s13138-024-00236-6
Monei, T., C Pedro, A. (2017). A systematic review of interventions for children presenting with dyscalculia in primary schools. Educational Psychology in Practice, 33(3), 277–293. https://doi.org/10.1080/02667363.2017.1289076
Rosenshine, B. (2012) Principles of Instruction: Research-based strategies that all teachers should know. American Educator, 36(1), pp. 12–39.
van Rooijen, M., Verhoeven, L., C Steenbergen, B. (2015). From numeracy to arithmetic: Precursors of arithmetic performance in children with cerebral palsy from 6 till 8 years of age. Research in Developmental Disabilities, 45–4c, 49–57. https://doi.org/10.1016/j.ridd.2015.07.001
Young-Leveridge, Jennifer (2011) rethinking the role of counting.
Faculty of Education The University of Waikato
-
- Using fingers, gestures and manipulatives to enable interaction with quantities and support number understanding and conservation.
- Counting on from a given number rather than going through all numerals. For example, knowing that if you wish to add 3 to 7 you start at the number 7.
- Children move on to being able to recall from a retrieval network of approaches for example:
A child may connect 6 + 4 = 10 to 4 + 6 = 10 and the inverse operation of 10 – 6 = 4 and relations to double 5 = 10 as well as 6 + ? = 10.
The study carried out by Leuenbeerger et al emphasise the importance of developing individualized learning programs for students who have difficulty acquiring maths proficiency.
Two pitfalls to avoid is that of split attention and the redundancy effect. Students who are already compromised by their access will find it difficult to attend to two things at once and can become distracted by extra information which does not explicitly relate to the computation (Sweller et al 2011). It is tempting to try to motivate students who are struggling by including exciting media or other inputs to gain attention, but if the student’s attention is diverted towards information that is not part of the learning objective such strategies are doomed to failure.
Baroody (2006) identified three phases that children go through when learning early maths operations as follows:
-
- Counting strategies such an object manipulation, using fingers etc
- Reasoning strategies which involve using known information to deduce answers.
- Mastery where the student has automatic recall of number facts.
It is important to note that students with physical and communication difficulties are often unable to experience phase one which might go some way to explaining why problems with number persist with this group.
Baroody goes on to explain that early operations are fact-retrieval skills, which we know the cohort of students we are referring to struggle with. He describes the fact-retrieval component of the brain as being separate from the conceptual and reasoning components of the brain. He goes on to suggest that learning number by rote requires more time and effort then recognising through establishing patterns and relationships. He argues that well connected factual knowledge is easier to retain than learning facts in isolation. He concludes that students who have difficulties mastering number should be provided with flexible options and routes through conceptual understanding and strategic mathematical teaching through purposeful instruction and guided inquiry.
Hargreaves et al (2025) identify a problem experienced by low-attaining students in that their motivation for learning becomes blocked by a sense of incompetency with subsequent negative impact on learning outcomes as students become focussed on their distress rather than in engaging in learning. This suggests that we need to focus on instruction that creates success rather than repeated failure.
The 2021 OFSTED review of mathematics identified three areas of mathematical knowledge as follows

The evidence suggests that students who rely on AAC (Augmentative and Alternative Communication) may have better procedural and conditional knowledge than they do declarative knowledge. This may be because the latter places more demands on retrieval from long-term memory and manipulation in working memory whilst procedural and conditional knowledge are less reliant on recall and can more easily become automated, scaffolded and coached through guided practice. A missed fact can stall a whole problem whereas a student might guess, reason, or use supports to carry out a procedure or choose a strategy without needing full memory access. OFSTED recommend the sequencing of declarative and procedural knowledge together rather than in a linear fashion which makes declarative knowledge a precursor to procedural knowledge.
Familiarity with the facts helps with learning and understanding but familiarity with method helps to make associated facts firm and precise in the mind.
https://www.gov.uk/government/publications/research-review-series- mathematics/research-review-series-mathematics
Bailey et. Al. (2020) focussed on strengthening conceptual and procedural foundations of arithmetic. This involved delivering structured lessons emphasising deep understanding of number concepts (such as place value and the meaning of operations) in addition to rote procedures boosted arithmetic (declarative) outcomes. However, they found that gains faded unless long-term strategies of a similar nature were put in place. In addition to fluency drills the intervention supported engagement with procedural problem-solving tasks without time pressure.
Ncube and Luneta (2025) found that concept-based instruction (CBI) improved learner performance by promoting deeper understanding of underlying principles rather than rote memorisation. The intervention focused on developing conceptual understanding of the mathematics of functions, rather than basic numeracy operations, aiming to improve higher-level thinking across ideas.
How can we support the cohort of students who have movement and communication difficulties?
By the nature of their physical difficulties this group of students are unable to develop their maths skills through early motor exploratory activity or from engaging with manipulatives. This suggests that we need a different approach to maths instruction for this group and that we must find a way to offer them these early learning routes in ways that are accessible to them.
Having repeatedly observed students failing to get beyond the numeral 10, and sometimes 5, using the traditional routes of counting and number bonds first, an alternative approach must be sought. Over the past few years, I have been working with many students in different ways, and I cannot prescribe a one-fits-all approach. It may help to look at a range of different approaches and how they might help or hinder the development of maths skills.
In the following table the AAC student refers to students who have physical and communication difficulties:
| Approach | Advantages for allstudents | Disadvantage s for allstudents | Implications for disabled/AACstudents |
| Mastery Model Description: Students must fully understand a concept before moving on. | Promotes deep learning and reduces gaps in understanding. | Difficult to maintain focus in a class of students who are at different levels of mastery. | AAC students rarely learn in a linear fashion so may be impeded by a method that required skills to be built in a prescribed way. |
| Inquiry-Based Learning Description: Students explore and discover mathematical ideas through guided investigation. | Students explore and discover mathematical ideas through guided investigation. | Relies on a high level of teacher skill in terms of student needs and individualisation. Students need to be motivated. | AAC students will often lack the prerequisite skills for independent investigation because they do not have the technology and/or support to be able to develop their investigative skills. |
| Direct Instruction Description: Teacher-led, structured lessons with clear objectives and practice. | Efficient for skill acquisition and procedural fluency provided the student is able to converge with the teaching process. | Relies on the teacher having regular checks of progress through testing or some othermechanism. Not easy to individualise learning needs. | The AAC student could quickly be left behind because the huge amount of differentiation an dadaptive teaching required may be difficult to achieve in a busy classroom environment. |
| Socratic Method Description: Uses questioning to stimulate critical thinking and uncover understanding. | Encourages deep reasoning and dialogue. | Requires significant confidence on the part of students and teachers.Scaffolds and prompts will be important. | The AAC student can benefit from this approach provided they have appropriate prompts and scaffolds (such as multiple-choice options) so that they can consider choices rather than having to‘think laterally’. |
| Cognitive Apprenticeship Description: Learners observe expert thinking, then practice with guidance. | Makes thinking visible and supports skill development. | Requires guidance for students to be able to progress. | The AAC student is really supported by this approach as it is individualised and the student benefits from continual guidance. |
| Spiral Curriculum Description: Concepts are revisited at increasing levels of complexity | Students revisit concepts regularly at increasing levels of difficulty so that their understanding deepens. | May feel repetitive for student who grasp concepts quickly. | AAC students can benefit from the repetition with the variety of incremental levels of difficulty being introduced. |
| Network Model Description:Concepts are interconnected in a web-like structure. | Encourages flexible thinking and deep understanding through relationship between ideas. | Students may become lost in a web of inter connections that might not be intuitive for them. | AAC students can benefit from drawing on their non-counting strengths to support the development of counting skills. |
| Concrete·Pictori al·Abstract (CPA) Description: Progresses from hands-on manipulatives to visual representations to symbolic notation. | Supports conceptual development and scaffolds learning. | Assumes that all students follow the same trajectory from concrete to pictorial to symbolic. | AAC students generally fall at the first post with this approach as they are often unable to engage with the early, hands-on stage. |
| Problem-Based Learning (PBL) Description: Learning is driven by solving real- world or complex problems. | Encourages application af knowledge through real world situations and collaborative learning. | Can be difficult to extract the mathematics needed to solve the real- world problem. | AAC students can benefit from being able to apply mathematical principles to real world problems BUT this approach often involves several stages which the AAC student needs to be supported through and able to refer to as they proceed through the problem-solving process. |
| Constructivist Model Description: Learners build their own understanding through experience and reflection. | Learners build their own understanding through experience and reflection. | Very dependent on the quality and depth of the learner’s day- to-dayexperiences. | The AAC student may be left floundering by this approach because they may not have the same level of world experience as their peers and can then quickly be left behind.Building experiences is essential if this approach is to be used. |
From this analysis the approaches most suited to the students who rely on AAC are:
-
- The Socratic method provided appropriate scaffolds are in place
-
- The Cognitive Apprenticeship approach provided appropriate scaffolds and models are in place.
-
- The Spiral Curriculum which enables repetition at spaced intervals with increments of new learning within already familiar approaches.
-
- The Network model which enables students to use their existing strengths to develop further skill and to make connections.
-
- The Problem-based learning model which connects mathematical principles to real world situations.
None of these models place the skill developments of counting and number bonds as prerequisites to learning. Instead, they foster the development of more generalised knowledge such as:
-
- Knowing which operation you need to use.
-
- Being able to discern patterns.
-
- Being able to orient in space and identify shape and, measure.
-
- Having an ability to discern quantity.
-
- Being able to connect ideas.
Potential Solutions for students who rely on AAC and/or have physical and communication difficulties
In the following example the student can use eye gaze, switches or other access to technology to investigate number and demonstrate understanding. If they need an answer it is there. The blue number plus any white number equals the blue number above the white number. This gives that AAC student the opportunity to practice skills repeatedly but in a variety of settings allowing generalisation and skills building to take place.
The most important point about these activities is that they allow the student to work independently without too much physical effort and in the most time effective way. Monei and Pedro (2017) confirm that strategies that reduce working memory effort are the most effective. With a student population that relies on assistive technology to achieve learning it is essential that the design of programs incorporate ease of access to preserve working memory as well as supporting independent access.
Independent working does not mean unsupported working. The student still needs to be scaffolded by a more knowledgeable other be it their teacher, parent, sibling, friend or teaching assistant.

In the following example the concept of plus 2 is being demonstrated so that the AAC student can practice that skill:

Hopkins et al (2022) found that many students use min-counting (counting on from the smallest number) but they maintain that this strategy is less effective than retrieval (automatic recall). A third group of students used decomposition which involves breaking complex problems down into simpler steps such as 345 – 12 = 345-10 =335 -2 = 333. Since retrieval is a difficult skill for AAC users to master (on account the time and repetition needed), decomposition may present a more workable solution. However, the breaking down of steps, in itself, could compromise working memory.
In the following example the steps are kept on the same page, but the cells end up being very small so that access may be compromised.

A reasonable adjustment for a student that still struggles with counting is to provide the following supports:
 |
 |
I have often been challenged in the past on recommending this kind of support as it is seen as cheating because the students are being given the answer. This is far from the truth. They still must understand the rules by which the support operates, and they then must select the correct support. What this also gives them is the repeated exposure that they need as a scaffold on the way to independent mental operations. It is vital that you teach before you test.

Constant checking to see if a student understands can be undermining, especially for disabled students. Valuable teaching time can be wasted with testing something that has not yet been sufficiently modelled and scaffolded. Unless you have first modelled (shown the student how a maths problem needs to be solved) and then scaffolded learning (given the student the problem but then given them hints to be able to solve the problem), you should not be testing.
Gervasoni (n.d) identifies five key skills that lead to confidence with number as follows:
1. Rote counting: Rote counts the number sequence to at least 20.

-
- Counting collections: Confidently counts a collection of around 20 objects.

-
- Counts forwards and backwards from various starting points between 1 and 100; knows numbers before and after a given number.

-
- Counting from 0 by 2s, 5s, and 10s: Can count from 0 by 2s, 5s, and 10s to a given target.

-
- Counting from x (where x>0) by 2s, 5s, and 10s: Can count from x by 2s, 5s, and 10s to a given target.

-
- Extending and Applying: Can count from a non-zero starting point by any single digit number, and can apply counting skills in practical tasks”

Although repetition is vital it is much more effective if it is carried out with variety. Counting the same 5 things every day does not enable generalisation to all things that are 51. Repetition with variety is encapsulated in several approaches including: mastery, scaffolding, spiral, and spacing. Let your variety include the introduction of more complex concepts than those that already appear to be grasped. For example, even if you feel a student can only count to 3, teach them to 10. 20 and beyond. This will give them a sense of progression and avoid students glossing over through boredom and lack of motivation. This is an example of teaching the same understanding in different ways:
 |
 |
 |
Explicit instruction in the strategies needed to complete these tasks without the distraction of contextualisation may be helpful for this cohort of students. However, if the student is showing no improvement an alternative approach may be required and should be integral to all teaching and learning for all students.
Rosenshine (2012) identifies 12 principles of instruction that should be considered as follows:
-
- Review previous learning before going on to new learning.
- Present new material in small steps with student practice after each step.
- Ask many questions so that students experience guided practice.
- Provide models (worked examples)
- Guide students practice with questioning, providing additional information, explaining each step, correcting errors and supporting students in working out problems.
- Check for student understanding and reteach or reframe if necessary.
- Obtain a high success rate. Aim for 80% success rate.
- Provide scaffolds for difficult tasks. These are temporary supports that are gradually withdrawn as the student gains in confidence and ability.
- Require and monitor independent practice.
- Engage students in weekly and monthly review (spaced learning)
Spaced learning has been found to be a productive way to embed learning but has yet to be fully incorporated into curriculum delivery in the UK. It involves returning to learning several times after a set time. In each return the time is longer.
https://www.tes.com/magazine/tes-explains/what-spaced-learning
In our desire to ensure that a student has grasped basic understanding before we move them on to more complex, reasoning based learning we may be further reducing the learning potential of students who may need another route into learning than is traditionally achieved through practice and rote learning. Spaced learning may be another route to grounded learning.
CandLE is developing a ‘thinking skills’ maths program which exposes students to number in incidental ways and always with an application based in real world experiences as well as supporting the understanding of concepts. This is an example of consolidating some previous work on shapes and introducing size and measure with number being incidentally used (repetition with variety and spaced learning).
 |
 |
 |
 |
Using a story about a family that is buying a house, creating a garden then going on holiday, we contextualise maths into a real-world situation. We don’t expect the student to use recall or retrieval. We give them a number square or a calculator for that but we do want them to know how to work out the answer to the problem :
 |
 |
 |
 |
 |
Here we are recapping measure before going on to use number in a context using estimation and developing world knowledge:
 |
 |
 |
 |
 |
 |
 |
 |
All the maths problems shown have been completed by students who still struggle with counting to 10 but, by working with broader maths concepts they are beginning to consolidate basic numeracy incidentally.
Researchers at Nottingham University found that improving children’s multiplication fact recall through retrieval practice doesn’t equate to improving their ability to use the multiplication facts they know. Children who can recall a multiplication fact such as 5 x 7 = 35, may not be able to use this fact to solve a problem such as “Tara has 7 books. Ravi has 4 times as many. How many books do they have together”. (Guy et al 2025)
The expectation in the UK is that students should know their times tables by the end of year 4. Given that students with physical and communication difficulty may take up to six times longer than their non-disabled peers to acquire knowledge that needs to be rote learnt this cohort could be in their mid-20’s before this is accomplished. The length of extra time calculation is based on CandLE findings when preparing for exams and timing student responses. By extension it can be inferred that it could also take a protracted length of time to achieve number bonds at a basic level. This is even if the students are not further disadvantaged by the fact that taking longer will have a negative impact on working memory and may make rote learning an even lengthier process if it is achievable at all.
So, let’s move on beyond basic counting and number fact recall and support students to experience mathematical concepts in different ways. Allow them to use calculators, number lines, number squares and multiplication squares to get over the counting and fact recall hurdle. Instead, let them focus on how the problem should be managed.
References
Bailey, D. H., Fuchs, L. S., Gilbert, J. K., Geary, D. C., C Fuchs, D. (2020). Prevention: Necessary But Insufficient? A 2-Year Follow-Up of an Effective First-Grade Mathematics Intervention. Child Development, S1(2), 382–400. https://doi.org/10.1111/cdev.13175
Baroody, A.J. (2006) ‘Why children have difficulties mastering the basic number combinations and how to help them’, Teaching Children Mathematics, 13(1), pp. 22–31.
Critten, V., Campbell, E., Farran, E., C Messer, D. (2018). Visual perception, visual-spatial cognition and mathematics: Associations and predictions in children with cerebral palsy. Research in Developmental Disabilities, 80, 180–191. https://doi.org/10.1016/j.ridd.2018.06.007
Development of early numeracy performance in children with cerebral palsy: The influence of cognitive and motor factors. (2015). https://hdl.handle.net/2066/140585
Developmental Disabilities, 5c(6), 442–457. https://doi.org/10.1352/1934- 9556-56.6.442
Flores, P., Coelho, E., Mourão-Carvalhal, M. I., C Forte, P. (2023). Association between motor and math skills in preschool children with typical development: Systematic review. In Frontiers in Psychology (Vol. 14). Frontiers Media S.A. https://doi.org/10.3389/fpsyg.2023.1105391
Hargreaves, E., Quick, L. and Buchanan, D. (2025) ‘“This is too boring”: a life-history approach to primary pupils’ distress and lack of motivation for school-work’, Pastoral Care in Education, pp. 1–19.
doi: 10.1080/02643944.2025.2454650
Gervasoni, A. (n.d.). KEY TRANSITIONS IN COUNTING DEVELOPMENT FOR YOUNG CHILDREN WHO EXPERIENCE DIFFICULTY.
Guy, N., Cragg, L. C Gilmore, C., 2025. Learning, using and applying multiplication facts: Insights from research. Chartered College of Teaching, 19 May [online]. Available at: https://my.chartered.college/impact_article/learning-using-and-applying- multiplication-facts-insights-from-research/ [Accessed 1 Aug. 2025].
Sweller, J., Ayres, P., C Kalyuga, S. (2011). Cognitive Load Theory. Springer.
→ See Chapter 4: Redundancy Effect.
Leuenberger, D., Diener, M., Wehren-Müller, M., Hofmann-Villiger, A., Vogt, F., C Moser Opitz, E. (2024). Fostering Computation Competence with
Non-Counting Strategies and Conceptual Subitizing in Grade 1: An Intervention Study in Inclusive Classrooms. Journal Fur Mathematik- Didaktik, 45(2). https://doi.org/10.1007/s13138-024-00236-6
Monei, T., C Pedro, A. (2017). A systematic review of interventions for children presenting with dyscalculia in primary schools. Educational Psychology in Practice, 33(3), 277–293. https://doi.org/10.1080/02667363.2017.1289076
Rosenshine, B. (2012) Principles of Instruction: Research-based strategies that all teachers should know. American Educator, 36(1), pp. 12–39.
van Rooijen, M., Verhoeven, L., C Steenbergen, B. (2015). From numeracy to arithmetic: Precursors of arithmetic performance in children with cerebral palsy from 6 till 8 years of age. Research in Developmental Disabilities, 45–4c, 49–57. https://doi.org/10.1016/j.ridd.2015.07.001
Young-Leveridge, Jennifer (2011) rethinking the role of counting.
Faculty of Education The University of Waikato